
AllQuestion and Answers: Page 1533
Question Number 58195 Answers: 2 Comments: 0
Question Number 58193 Answers: 0 Comments: 0
Question Number 58187 Answers: 0 Comments: 0
Question Number 58185 Answers: 0 Comments: 0
$${find}\:\int\:\:\:\frac{{xdx}}{{cosx}\:+{sin}\left(\mathrm{2}{x}\right)} \\ $$
Question Number 58184 Answers: 0 Comments: 0
$${find}\:\:\int\:\:\:\:\:\:\frac{{xdx}}{{sinx}\:+{cos}\left(\mathrm{2}{x}\right)} \\ $$
Question Number 58178 Answers: 0 Comments: 0

Question Number 58177 Answers: 2 Comments: 0
Question Number 58176 Answers: 1 Comments: 0
Question Number 58175 Answers: 1 Comments: 0
Question Number 58174 Answers: 0 Comments: 2
Question Number 58171 Answers: 1 Comments: 0
Question Number 58168 Answers: 2 Comments: 0
$${find}\:\int\:\:\:\:\frac{\sqrt{{tanx}}}{{sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$
Question Number 58156 Answers: 1 Comments: 0
Question Number 58154 Answers: 1 Comments: 0
Question Number 58153 Answers: 1 Comments: 0
Question Number 58145 Answers: 1 Comments: 0
Question Number 58135 Answers: 1 Comments: 0
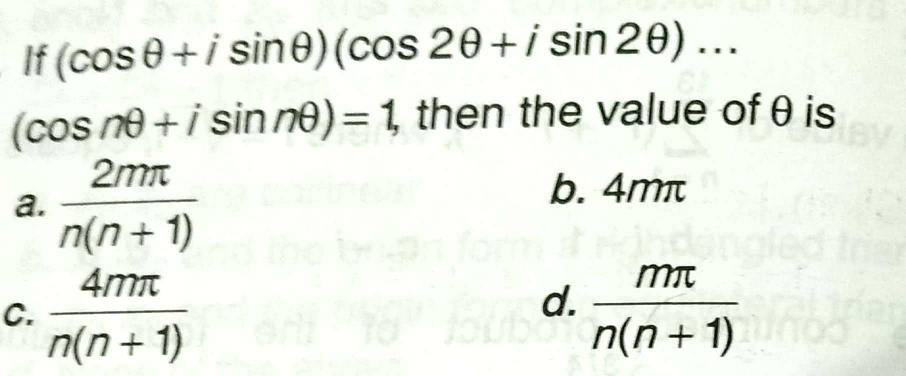
Question Number 58132 Answers: 2 Comments: 1
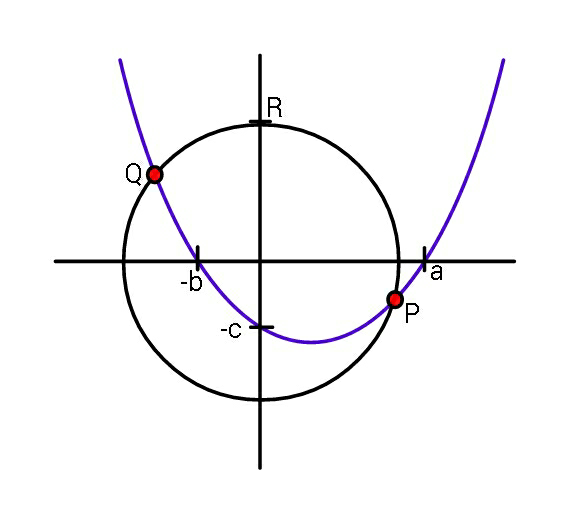
Question Number 58113 Answers: 0 Comments: 1
Question Number 58103 Answers: 1 Comments: 0
Question Number 58097 Answers: 2 Comments: 0
Question Number 58092 Answers: 3 Comments: 0
$$\mathrm{6}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{5}=\mathrm{0} \\ $$
Question Number 58091 Answers: 2 Comments: 0
Question Number 58090 Answers: 1 Comments: 0
Question Number 58084 Answers: 0 Comments: 3

Question Number 58079 Answers: 1 Comments: 0
Pg 1528 Pg 1529 Pg 1530 Pg 1531 Pg 1532 Pg 1533 Pg 1534 Pg 1535 Pg 1536 Pg 1537
