
AllQuestion and Answers: Page 1530
Question Number 58614 Answers: 2 Comments: 0
Question Number 58612 Answers: 1 Comments: 0
Question Number 58609 Answers: 1 Comments: 0

Question Number 58600 Answers: 2 Comments: 0
Question Number 58595 Answers: 1 Comments: 0

Question Number 58592 Answers: 1 Comments: 0
Question Number 58587 Answers: 0 Comments: 0
Question Number 58584 Answers: 0 Comments: 0
Question Number 58576 Answers: 2 Comments: 0
Question Number 58569 Answers: 1 Comments: 0
Question Number 58568 Answers: 2 Comments: 1
Question Number 58567 Answers: 0 Comments: 1
Question Number 58547 Answers: 1 Comments: 1

Question Number 58558 Answers: 1 Comments: 0
Question Number 58530 Answers: 2 Comments: 0
Question Number 58521 Answers: 1 Comments: 0
Question Number 58519 Answers: 1 Comments: 1

Question Number 58512 Answers: 1 Comments: 1
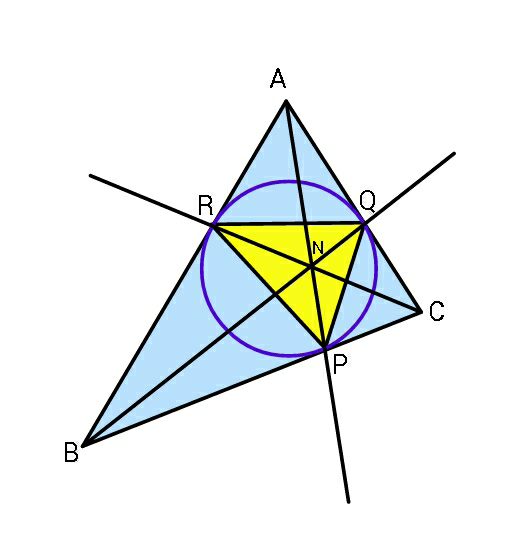
Question Number 58508 Answers: 1 Comments: 0

Question Number 58501 Answers: 2 Comments: 0
Question Number 58500 Answers: 2 Comments: 0
Question Number 58493 Answers: 1 Comments: 0

Question Number 58488 Answers: 0 Comments: 2
Question Number 58487 Answers: 0 Comments: 3
Question Number 58480 Answers: 0 Comments: 2

Question Number 58479 Answers: 0 Comments: 1

Pg 1525 Pg 1526 Pg 1527 Pg 1528 Pg 1529 Pg 1530 Pg 1531 Pg 1532 Pg 1533 Pg 1534
