Question and Answers Forum

AllQuestion and Answers: Page 1529

Question Number 58346 Answers: 2 Comments: 0

∫((cos(x))/(cos(2016°+cos(x)))×dx

$$\int\frac{\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{cos}}\left(\mathrm{2016}°+\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)\right.}×\boldsymbol{\mathrm{dx}} \\ $$

Question Number 58354 Answers: 1 Comments: 0

let U_n =((1^2 +2^2 +3^2 +....+n^2 )/(1^4 +2^4 +3^4 +....+n^4 )) 1)find lim_(n→+∞) U_n 2) calculate Σ_(n=1) ^∞ U_n

$${let}\:{U}_{{n}} =\frac{\mathrm{1}^{\mathrm{2}} \:+\mathrm{2}^{\mathrm{2}} \:+\mathrm{3}^{\mathrm{2}} \:+....+{n}^{\mathrm{2}} }{\mathrm{1}^{\mathrm{4}} \:+\mathrm{2}^{\mathrm{4}} \:+\mathrm{3}^{\mathrm{4}} \:+....+{n}^{\mathrm{4}} } \\ $$$$\left.\mathrm{1}\right){find}\:{lim}_{{n}\rightarrow+\infty} {U}_{{n}} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:{U}_{{n}} \\ $$

Question Number 58319 Answers: 1 Comments: 0

∫x^n (lnx)^n dx

$$\int{x}^{{n}} \left(\mathrm{ln}{x}\right)^{{n}} {dx} \\ $$

Question Number 58309 Answers: 2 Comments: 3

Prove that lim_(x→0) ((1−cos(x)cos(x/2)cos(x/3)...)/x^2 )=(π^2 /(12))

$${Prove}\:{that}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{1}−{cos}\left({x}\right){cos}\left({x}/\mathrm{2}\right){cos}\left({x}/\mathrm{3}\right)...}{{x}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Question Number 58299 Answers: 1 Comments: 1

find ∫ (dx/((x^2 +x+1)^(3/2) ))

$${find}\:\int\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$

Question Number 58286 Answers: 0 Comments: 1

A small body with temperature θ and absorbtivity τ is placed in a large evaluated capacity whose interior walls are at a temperature θ_w . when θ_w −θ is small, show that the rate of heat transfer by radiation is Q^• = 4θ_w ^3 Aτδ(θ_w −θ).

$$\mathrm{A}\:\mathrm{small}\:\mathrm{body}\:\mathrm{with}\:\mathrm{temperature}\:\theta\:\mathrm{and} \\ $$$$\mathrm{absorbtivity}\:\tau\:\mathrm{is}\:\mathrm{placed}\:\mathrm{in}\:\mathrm{a}\:\mathrm{large}\: \\ $$$$\mathrm{evaluated}\:\mathrm{capacity}\:\mathrm{whose}\:\mathrm{interior}\: \\ $$$$\mathrm{walls}\:\mathrm{are}\:\mathrm{at}\:\mathrm{a}\:\mathrm{temperature}\:\theta_{\mathrm{w}} . \\ $$$$\mathrm{when}\:\:\:\:\theta_{\mathrm{w}} −\theta\:\:\:\:\mathrm{is}\:\:\mathrm{small},\:\mathrm{show}\:\mathrm{that}\:\mathrm{the} \\ $$$$\mathrm{rate}\:\mathrm{of}\:\mathrm{heat}\:\mathrm{transfer}\:\mathrm{by}\:\mathrm{radiation}\:\mathrm{is} \\ $$$$\:\:\:\:\:\overset{\bullet} {\mathrm{Q}}=\:\mathrm{4}\theta_{\mathrm{w}} ^{\mathrm{3}} \mathrm{A}\tau\delta\left(\theta_{\mathrm{w}} −\theta\right). \\ $$

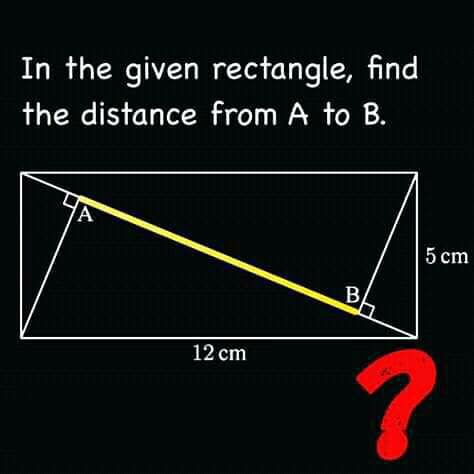
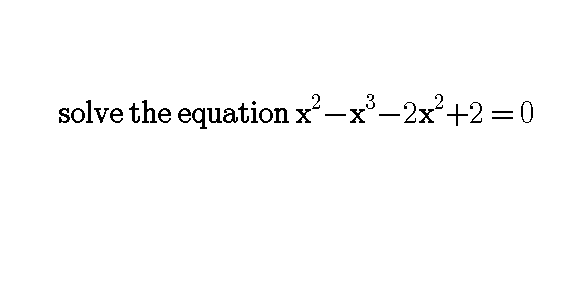
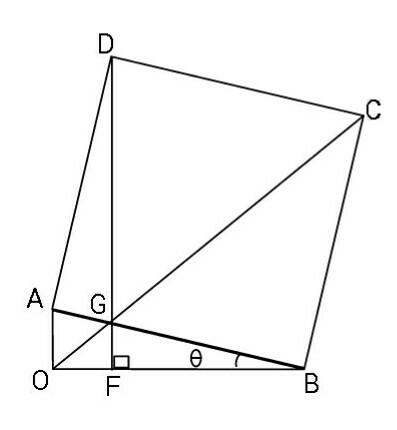
Question Number 58282 Answers: 1 Comments: 0

A circle tangents to :x and y axes and x^(1/2) +y^(1/2) =a^(1/2) .find its radious.

Question Number 58276 Answers: 0 Comments: 0

Question Number 58267 Answers: 0 Comments: 13

lim_(x→0) [((1−cos (x)cos (2x)cos (3x)cos (4x))/x^2 )]

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\frac{\mathrm{1}−\mathrm{cos}\:\left({x}\right)\mathrm{cos}\:\left(\mathrm{2}{x}\right)\mathrm{cos}\:\left(\mathrm{3}{x}\right)\mathrm{cos}\:\left(\mathrm{4}{x}\right)}{{x}^{\mathrm{2}} }\right] \\ $$

Question Number 58259 Answers: 4 Comments: 4

a .∫ (dx/(2sin^2 x+3tg^2 x))=? b .∫(( 1+(x)^(1/3) )/(1+(√x)+(x)^(1/3) +(x)^(1/6) ))dx=? c .∫ ((cosx)/(1+cos2x))dx=? d .∫ ((sin^2 x)/((√2)+(√3).cos^2 x))dx=?

Question Number 58257 Answers: 1 Comments: 1

Question Number 58254 Answers: 1 Comments: 0

The line 3x−2y−5=0 is parallel to a diameter of a circle x^2 +y^2 −4x+2y−4=0. find the equation of the diameter.

$$\mathrm{The}\:\mathrm{line}\:\mathrm{3x}−\mathrm{2y}−\mathrm{5}=\mathrm{0}\:\mathrm{is}\:\mathrm{parallel}\:\mathrm{to}\:\mathrm{a}\:\mathrm{diameter} \\ $$$$\mathrm{of}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{4x}+\mathrm{2y}−\mathrm{4}=\mathrm{0}.\:\mathrm{find}\:\mathrm{the} \\ $$$$\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{diameter}. \\ $$

Question Number 58253 Answers: 1 Comments: 0

There are 100, 150 and 250 students in forms one, two and three, respectively in a school. If the mean ages of tbe students in the forms are 15.6 years, 16.8 years and 18years respectively, find i. the total number of students in the forms ii. correct to one decimal place, the mean age of all the students

$$\mathrm{There}\:\mathrm{are}\:\mathrm{100},\:\mathrm{150}\:\mathrm{and}\:\mathrm{250}\:\mathrm{students}\:\mathrm{in} \\ $$$$\mathrm{forms}\:\mathrm{one},\:\mathrm{two}\:\mathrm{and}\:\mathrm{three},\:\mathrm{respectively} \\ $$$$\mathrm{in}\:\mathrm{a}\:\mathrm{school}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{mean}\:\mathrm{ages}\:\mathrm{of}\:\mathrm{tbe}\:\mathrm{students}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{forms}\:\mathrm{are}\:\mathrm{15}.\mathrm{6}\:\mathrm{years},\:\mathrm{16}.\mathrm{8}\:\mathrm{years}\:\mathrm{and} \\ $$$$\mathrm{18years}\:\mathrm{respectively},\:\mathrm{find} \\ $$$$\mathrm{i}.\:\mathrm{the}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{students}\:\mathrm{in}\:\mathrm{the}\:\mathrm{forms} \\ $$$$\mathrm{ii}.\:\mathrm{correct}\:\mathrm{to}\:\mathrm{one}\:\mathrm{decimal}\:\mathrm{place},\:\mathrm{the}\:\mathrm{mean} \\ $$$$\mathrm{age}\:\mathrm{of}\:\mathrm{all}\:\mathrm{the}\:\mathrm{students} \\ $$

Question Number 58250 Answers: 1 Comments: 0

∫_( 0) ^( 1) (((3x^3 − x^2 + 2x − 4)/(√(x^2 − 3x + 2)))) dx

$$\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\:\left(\frac{\mathrm{3x}^{\mathrm{3}} \:−\:\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{2x}\:−\:\mathrm{4}}{\sqrt{\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{3x}\:+\:\mathrm{2}}}\right)\:\mathrm{dx} \\ $$

Question Number 58249 Answers: 0 Comments: 0

I_n ^ =∫_0 ^(π/2) cos^n xcos(nx)dx then show that I_1 ,I_2 ,I_3 ....are in G.P

$$\overset{} {{I}}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{{n}} {xcos}\left({nx}\right){dx} \\ $$$${then}\:{show}\:{that}\:{I}_{\mathrm{1}} ,{I}_{\mathrm{2}} ,{I}_{\mathrm{3}} ....{are}\:{in}\:{G}.{P} \\ $$

Question Number 58248 Answers: 1 Comments: 0

leg A_1 ,A_2 ,...A_n and H_1 ,H_2 ,...H_n are n A.M′S and H.M′S respectively between a and b prove that A_r H_(n−r+1) =ab n≥r≥1

$${leg}\:{A}_{\mathrm{1}} ,{A}_{\mathrm{2}} ,...{A}_{{n}} \:{and}\:{H}_{\mathrm{1}} ,{H}_{\mathrm{2}} ,...{H}_{{n}} \:{are}\:{n}\:{A}.{M}'{S}\: \\ $$$${and}\:{H}.{M}'{S}\:{respectively}\:{between}\:{a}\:{and}\:{b} \\ $$$${prove}\:{that}\:{A}_{{r}} {H}_{{n}−{r}+\mathrm{1}} ={ab} \\ $$$$\:{n}\geqslant{r}\geqslant\mathrm{1} \\ $$

Question Number 58247 Answers: 0 Comments: 0

lim_(n→∞) ((S_1 S_n +S_2 S_(n−1) +S_3 S_(n−2) +...+S_n S_1 )/(S_1 ^2 +S_2 ^2 +...+S_n ^2 )) when S_n is sum of infinite series whose first term=n and common ratio (1/(n+1)) find the value of limit

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{S}_{\mathrm{1}} {S}_{{n}} +{S}_{\mathrm{2}} {S}_{{n}−\mathrm{1}} +{S}_{\mathrm{3}} {S}_{{n}−\mathrm{2}} +...+{S}_{{n}} {S}_{\mathrm{1}} }{{S}_{\mathrm{1}} ^{\mathrm{2}} +{S}_{\mathrm{2}} ^{\mathrm{2}} +...+{S}_{{n}} ^{\mathrm{2}} } \\ $$$${when}\:{S}_{{n}} \:{is}\:{sum}\:{of}\:{infinite}\:{series}\:{whose} \\ $$$${first}\:{term}={n}\:\:\:{and}\:{common}\:{ratio}\:\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$${find}\:{the}\:{value}\:{of}\:{limit} \\ $$

Question Number 58246 Answers: 1 Comments: 0

show that P=x^(9999) +x^(8888) +x^(7777) +x^(6666) +x^(5555) +x^(4444) +x^(3333) +x^(2222) +x^(1111) +1 Q=x^9 +x^8 +x^7 +x^6 +x^5 +x^4 +x^3 +x^2 +x+1 prove P is divisible by Q

$${show}\:{that} \\ $$$${P}={x}^{\mathrm{9999}} +{x}^{\mathrm{8888}} +{x}^{\mathrm{7777}} +{x}^{\mathrm{6666}} +{x}^{\mathrm{5555}} +{x}^{\mathrm{4444}} +{x}^{\mathrm{3333}} +{x}^{\mathrm{2222}} +{x}^{\mathrm{1111}} +\mathrm{1} \\ $$$${Q}={x}^{\mathrm{9}} +{x}^{\mathrm{8}} +{x}^{\mathrm{7}} +{x}^{\mathrm{6}} +{x}^{\mathrm{5}} +{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1} \\ $$$${prove}\:\:{P}\:\:{is}\:{divisible}\:{by}\:{Q} \\ $$

Question Number 58245 Answers: 1 Comments: 0

if log(a+b+c)=loga+logb+logc prove log(((2a)/(1−a^2 ))+((2b)/(1−b^2 ))+((2c)/(1−c^2 )))=log(((2a)/(1−a^2 )))+log(((2b)/(1−b^2 )))+log(((2c)/(1−c^2 )))

$${if}\:{log}\left({a}+{b}+{c}\right)={loga}+{logb}+{logc} \\ $$$${prove} \\ $$$${log}\left(\frac{\mathrm{2}{a}}{\mathrm{1}−{a}^{\mathrm{2}} }+\frac{\mathrm{2}{b}}{\mathrm{1}−{b}^{\mathrm{2}} }+\frac{\mathrm{2}{c}}{\mathrm{1}−{c}^{\mathrm{2}} }\right)={log}\left(\frac{\mathrm{2}{a}}{\mathrm{1}−{a}^{\mathrm{2}} }\right)+{log}\left(\frac{\mathrm{2}{b}}{\mathrm{1}−{b}^{\mathrm{2}} }\right)+{log}\left(\frac{\mathrm{2}{c}}{\mathrm{1}−{c}^{\mathrm{2}} }\right) \\ $$

Question Number 58240 Answers: 1 Comments: 2

i=∫dx/(ax^2 +bx+c)^(3/2)

$$\mathrm{i}=\int\mathrm{dx}/\left(\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$

Question Number 58239 Answers: 1 Comments: 0

lim_(x→0^+ ) (x^(1/x) )

$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left({x}^{\frac{\mathrm{1}}{{x}}} \right) \\ $$

Question Number 58238 Answers: 0 Comments: 0

∫_( 0) ^( 1) (((3x^3 − x^2 + 2x − 4)/(√(x^2 − 3x + 2)))) dx

$$\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\:\left(\frac{\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{3}} \:−\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:+\:\mathrm{2}\boldsymbol{\mathrm{x}}\:−\:\mathrm{4}}{\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:−\:\mathrm{3}\boldsymbol{\mathrm{x}}\:+\:\mathrm{2}}}\right)\:\:\boldsymbol{\mathrm{dx}} \\ $$

Question Number 58222 Answers: 2 Comments: 4

∫_0 ^1 x^x dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{x}} {dx} \\ $$

Question Number 58220 Answers: 1 Comments: 0

find ∫ (dx/((x^2 +x)(√(−x^2 +2x +3))))

$${find}\:\int\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}\right)\sqrt{−{x}^{\mathrm{2}} \:+\mathrm{2}{x}\:+\mathrm{3}}} \\ $$$$ \\ $$

Question Number 58216 Answers: 1 Comments: 1

The molar heat capacity of a metal at low temperature varies with the temperature according to the equation C = bθ + (a/H)θ^3 where a, b and H are constant. How much heat per mole is transfered during the process in which the temperature change from 0.01H to 0.02H ?

$$\mathrm{The}\:\mathrm{molar}\:\mathrm{heat}\:\mathrm{capacity}\:\mathrm{of}\:\mathrm{a}\:\mathrm{metal}\:\:\mathrm{at} \\ $$$$\mathrm{low}\:\mathrm{temperature}\:\mathrm{varies}\:\mathrm{with}\:\mathrm{the}\: \\ $$$$\mathrm{temperature}\:\mathrm{according}\:\mathrm{to}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\:\:\:\:\:\:\:\mathrm{C}\:=\:\mathrm{b}\theta\:+\:\frac{\mathrm{a}}{\mathrm{H}}\theta^{\mathrm{3}} \\ $$$$\mathrm{where}\:\mathrm{a},\:\mathrm{b}\:\mathrm{and}\:\mathrm{H}\:\mathrm{are}\:\mathrm{constant}. \\ $$$$\mathrm{How}\:\mathrm{much}\:\mathrm{heat}\:\mathrm{per}\:\mathrm{mole}\:\mathrm{is}\:\mathrm{transfered} \\ $$$$\mathrm{during}\:\mathrm{the}\:\mathrm{process}\:\mathrm{in}\:\mathrm{which}\:\mathrm{the}\: \\ $$$$\mathrm{temperature}\:\mathrm{change}\:\mathrm{from}\:\mathrm{0}.\mathrm{01H}\: \\ $$$$\mathrm{to}\:\mathrm{0}.\mathrm{02H}\:? \\ $$

Question Number 58212 Answers: 0 Comments: 0

let f(x) =∫_0 ^∞ e^(−x[t]) sin(xt)dt with x>0 1) find a explicit form for f(x) 2) let U_n =nf(n) find lim_(n→+∞) U_n and study the convergence of ΣU_n

$${let}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{x}\left[{t}\right]} \:{sin}\left({xt}\right){dt}\:\:\:{with}\:{x}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicit}\:{form}\:{for}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{let}\:{U}_{{n}} ={nf}\left({n}\right)\:\:\:{find}\:{lim}_{{n}\rightarrow+\infty} \:{U}_{{n}} \:\:\:{and}\:{study}\:{the}\:{convergence}\:{of}\:\Sigma{U}_{{n}} \\ $$

Pg 1524 Pg 1525 Pg 1526 Pg 1527 Pg 1528 Pg 1529 Pg 1530 Pg 1531 Pg 1532 Pg 1533

Contact: info@tinkutara.com