
AllQuestion and Answers: Page 1526
Question Number 59097 Answers: 0 Comments: 0
Question Number 59095 Answers: 1 Comments: 0
Question Number 59094 Answers: 1 Comments: 1

Question Number 59092 Answers: 1 Comments: 0
Question Number 59089 Answers: 1 Comments: 0

Question Number 59080 Answers: 0 Comments: 0

Question Number 59079 Answers: 0 Comments: 0

Question Number 59077 Answers: 0 Comments: 0

Question Number 59076 Answers: 0 Comments: 0

Question Number 59075 Answers: 0 Comments: 1

Question Number 59074 Answers: 0 Comments: 0

Question Number 59070 Answers: 3 Comments: 0

Question Number 59060 Answers: 2 Comments: 0

Question Number 59059 Answers: 0 Comments: 0

Question Number 59058 Answers: 2 Comments: 1

Question Number 59053 Answers: 0 Comments: 0
$${f}={v} \\ $$$${v}=\mathrm{47}×\mathrm{48} \\ $$$${f}=? \\ $$
Question Number 59052 Answers: 0 Comments: 0
Question Number 59050 Answers: 1 Comments: 0
Question Number 59049 Answers: 0 Comments: 1
Question Number 59040 Answers: 3 Comments: 0
Question Number 59023 Answers: 0 Comments: 0
Question Number 59021 Answers: 2 Comments: 10
Question Number 59018 Answers: 0 Comments: 1
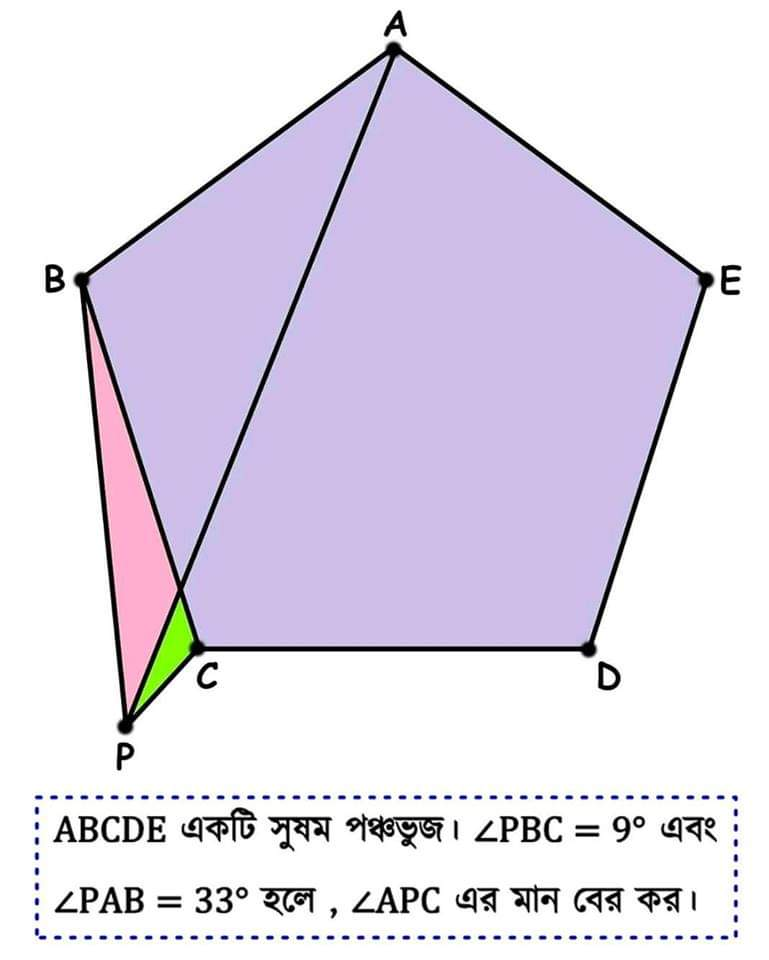
Question Number 59012 Answers: 3 Comments: 0
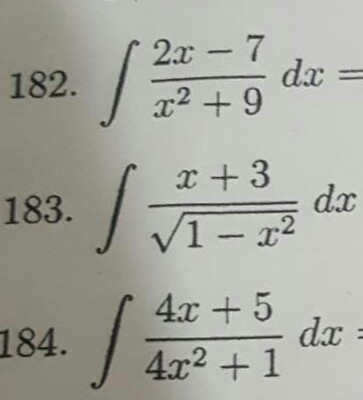
Question Number 59006 Answers: 0 Comments: 1
Question Number 59003 Answers: 0 Comments: 0

Pg 1521 Pg 1522 Pg 1523 Pg 1524 Pg 1525 Pg 1526 Pg 1527 Pg 1528 Pg 1529 Pg 1530
