
AllQuestion and Answers: Page 1519
Question Number 59842 Answers: 1 Comments: 3
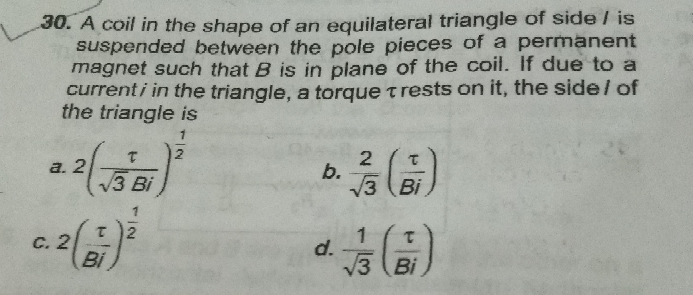
Question Number 59838 Answers: 1 Comments: 1
Question Number 59835 Answers: 1 Comments: 0

Question Number 59834 Answers: 1 Comments: 0

Question Number 59833 Answers: 1 Comments: 0

Question Number 59832 Answers: 0 Comments: 0

Question Number 59829 Answers: 2 Comments: 2

Question Number 59825 Answers: 0 Comments: 0

Question Number 59814 Answers: 1 Comments: 1

Question Number 59812 Answers: 1 Comments: 1
Question Number 59811 Answers: 1 Comments: 2
Question Number 59803 Answers: 0 Comments: 3

Question Number 59802 Answers: 0 Comments: 1

Question Number 59800 Answers: 2 Comments: 0
Question Number 59788 Answers: 2 Comments: 4
Question Number 59787 Answers: 2 Comments: 0

Question Number 59781 Answers: 0 Comments: 0

Question Number 59780 Answers: 1 Comments: 0
Question Number 59777 Answers: 0 Comments: 4

Question Number 59764 Answers: 1 Comments: 0
Question Number 59763 Answers: 1 Comments: 0
Question Number 59753 Answers: 2 Comments: 0
Question Number 59752 Answers: 1 Comments: 2

Question Number 59807 Answers: 1 Comments: 0
$$\int\frac{{x}−\mathrm{1}}{\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} }}\:{dx} \\ $$
Question Number 59733 Answers: 2 Comments: 2
Question Number 59732 Answers: 2 Comments: 0
Pg 1514 Pg 1515 Pg 1516 Pg 1517 Pg 1518 Pg 1519 Pg 1520 Pg 1521 Pg 1522 Pg 1523
