Question and Answers Forum

AllQuestion and Answers: Page 1515

Question Number 48659 Answers: 1 Comments: 0

Find x 3sec[2(x+(π/6))]= 4

$$\mathrm{Find}\:\mathrm{x} \\ $$$$\mathrm{3sec}\left[\mathrm{2}\left(\mathrm{x}+\frac{\pi}{\mathrm{6}}\right)\right]=\:\mathrm{4} \\ $$

Question Number 48656 Answers: 0 Comments: 3

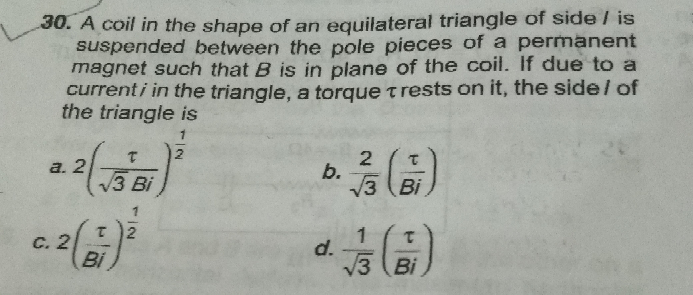
Question Number 48653 Answers: 1 Comments: 1

Question Number 48643 Answers: 1 Comments: 2

Question Number 48638 Answers: 1 Comments: 4

Question Number 48616 Answers: 0 Comments: 1

find four numbers such that the sum of every two and the sum of all four should be perfect squaresk

$${find}\:{four}\:{numbers}\:{such}\:{that}\:{the}\:{sum}\:{of}\:{every}\:{two}\:{and}\:{the}\:{sum}\:{of}\:{all}\:{four}\:{should}\:{be}\:{perfect}\:{squaresk}\: \\ $$

Question Number 48611 Answers: 1 Comments: 0

Question Number 48610 Answers: 0 Comments: 0

Question Number 48585 Answers: 0 Comments: 1

Who knows how to define a differential equation geometrically? I want to learn plz

$${Who}\:{knows}\:{how}\:{to}\:{define}\:{a}\: \\ $$$${differential}\:{equation}\:{geometrically}? \\ $$$${I}\:{want}\:{to}\:{learn}\:{plz} \\ $$

Question Number 48581 Answers: 1 Comments: 0

f(x)=[tan( π/4+x)^(1/x) ] =k is conntinous at x=0 then k=?

$${f}\left({x}\right)=\left[\mathrm{tan}\left(\:\pi/\mathrm{4}+{x}\right)^{\mathrm{1}/{x}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{k} \\ $$$${is}\:{con}\mathrm{ntinous}\:\mathrm{at}\:\mathrm{x}=\mathrm{0}\:\mathrm{then}\:\mathrm{k}=? \\ $$

Question Number 48567 Answers: 0 Comments: 1

Question Number 48560 Answers: 1 Comments: 1

Question Number 48559 Answers: 3 Comments: 0

Question Number 48553 Answers: 1 Comments: 2

In a hospital unit,there are 8 nurses and 5 physicians. 7 of them are female nurses and 3 of them are male physicians. what is the the probability of selecting a staff who is Nurse or Male? plzz help

$$\mathrm{In}\:\mathrm{a}\:\mathrm{hospital}\:\mathrm{unit},\mathrm{there}\:\mathrm{are}\:\mathrm{8}\:\mathrm{nurses} \\ $$$$\mathrm{and}\:\mathrm{5}\:\mathrm{physicians}.\:\mathrm{7}\:\mathrm{of}\:\mathrm{them}\:\mathrm{are} \\ $$$$\mathrm{female}\:\mathrm{nurses}\:\mathrm{and}\:\mathrm{3}\:\mathrm{of}\:\mathrm{them}\:\mathrm{are} \\ $$$$\mathrm{male}\:\mathrm{physicians}. \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{of} \\ $$$$\mathrm{selecting}\:\mathrm{a}\:\mathrm{staff}\:\mathrm{who}\:\mathrm{is}\:\mathrm{Nurse}\:\mathrm{or} \\ $$$$\mathrm{Male}? \\ $$$$\mathrm{plzz}\:\mathrm{help} \\ $$$$ \\ $$$$ \\ $$

Question Number 48543 Answers: 2 Comments: 0

The number of times the digit 3 will be written when listing the integers from 1 to 1000 is

$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{times}\:\mathrm{the}\:\mathrm{digit}\:\mathrm{3}\:\mathrm{will} \\ $$$$\mathrm{be}\:\mathrm{written}\:\mathrm{when}\:\mathrm{listing}\:\mathrm{the}\:\mathrm{integers} \\ $$$$\mathrm{from}\:\mathrm{1}\:\mathrm{to}\:\mathrm{1000}\:\mathrm{is} \\ $$

Question Number 48541 Answers: 1 Comments: 12

Question Number 48540 Answers: 2 Comments: 0

Question Number 48529 Answers: 3 Comments: 0

If cos A+cos B=m and sin A+sin B=n where m, n ≠0, then sin (A+B) is equal to

$$\mathrm{If}\:\:\mathrm{cos}\:{A}+\mathrm{cos}\:{B}={m}\:\mathrm{and}\:\mathrm{sin}\:{A}+\mathrm{sin}\:{B}={n} \\ $$$$\mathrm{where}\:{m},\:{n}\:\neq\mathrm{0},\:\mathrm{then}\:\mathrm{sin}\:\left({A}+{B}\right)\:\mathrm{is}\:\mathrm{equal} \\ $$$$\mathrm{to} \\ $$

Question Number 48528 Answers: 1 Comments: 0

The value of (√3) cot 20°− 4 cos 20° is

$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\sqrt{\mathrm{3}}\:\mathrm{cot}\:\mathrm{20}°−\:\mathrm{4}\:\mathrm{cos}\:\mathrm{20}°\:\:\mathrm{is} \\ $$

Question Number 48527 Answers: 2 Comments: 0

If xy + yz + zx = 1, then tan^(−1) x + tan^(−1) y + tan^(−1) z =

$$\mathrm{If}\:\:{xy}\:+\:{yz}\:+\:{zx}\:=\:\mathrm{1},\:\mathrm{then} \\ $$$$\mathrm{tan}^{−\mathrm{1}} {x}\:+\:\mathrm{tan}^{−\mathrm{1}} {y}\:+\:\mathrm{tan}^{−\mathrm{1}} {z}\:=\: \\ $$

Question Number 48526 Answers: 2 Comments: 0

The maximum and minimum values of a cos 2θ+ b sin 2θ are

$$\mathrm{The}\:\mathrm{maximum}\:\mathrm{and}\:\mathrm{minimum}\:\mathrm{values} \\ $$$$\mathrm{of}\:\:\:{a}\:\mathrm{cos}\:\mathrm{2}\theta+\:{b}\:\mathrm{sin}\:\mathrm{2}\theta\:\:\mathrm{are} \\ $$

Question Number 48525 Answers: 0 Comments: 0

Question Number 48524 Answers: 0 Comments: 0

Prime numbers differing by 2 are called _____.

$$\mathrm{Prime}\:\mathrm{numbers}\:\mathrm{differing}\:\mathrm{by}\:\mathrm{2}\:\mathrm{are} \\ $$$$\mathrm{called}\:\_\_\_\_\_. \\ $$

Question Number 48522 Answers: 1 Comments: 1

Question Number 48517 Answers: 3 Comments: 1

Question Number 48510 Answers: 0 Comments: 2

Pg 1510 Pg 1511 Pg 1512 Pg 1513 Pg 1514 Pg 1515 Pg 1516 Pg 1517 Pg 1518 Pg 1519

Contact: info@tinkutara.com