
AllQuestion and Answers: Page 1514
Question Number 59960 Answers: 1 Comments: 0

Question Number 59974 Answers: 1 Comments: 0

Question Number 59957 Answers: 0 Comments: 0

Question Number 59956 Answers: 0 Comments: 0

Question Number 59958 Answers: 0 Comments: 0

Question Number 59946 Answers: 1 Comments: 1

Question Number 59942 Answers: 1 Comments: 0
Question Number 59936 Answers: 1 Comments: 0

Question Number 59935 Answers: 0 Comments: 1
Question Number 59932 Answers: 0 Comments: 0

Question Number 59929 Answers: 0 Comments: 0
Question Number 59926 Answers: 2 Comments: 1

Question Number 59907 Answers: 0 Comments: 0

Question Number 59906 Answers: 0 Comments: 0
Question Number 59905 Answers: 0 Comments: 1
$$\int\left(\mathrm{2x}−\mathrm{1}\hat {\right)}\mathrm{20} \\ $$
Question Number 59904 Answers: 0 Comments: 0
$$\left(\mathrm{2x}−\mathrm{1}\hat {\right)}\mathrm{20} \\ $$
Question Number 59902 Answers: 0 Comments: 1
Question Number 59901 Answers: 0 Comments: 0
Question Number 59893 Answers: 0 Comments: 7
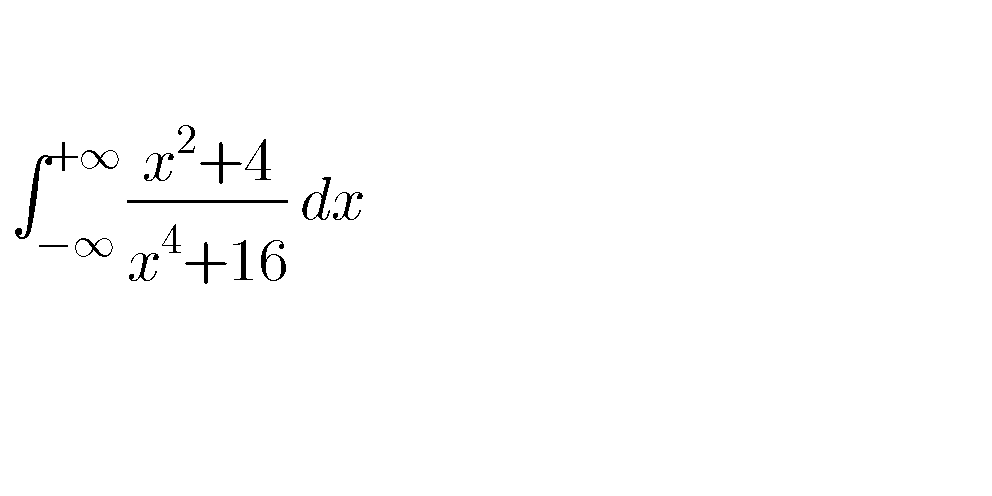
Question Number 59892 Answers: 2 Comments: 2
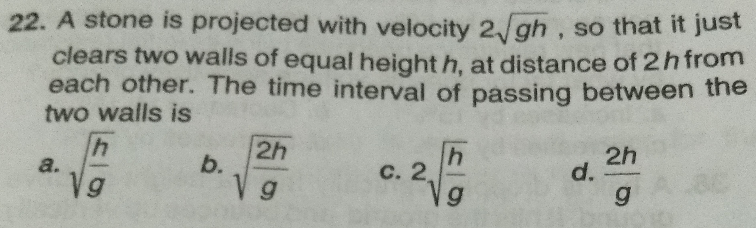
Question Number 59882 Answers: 0 Comments: 5
Question Number 59976 Answers: 2 Comments: 0
Question Number 59975 Answers: 1 Comments: 0

Question Number 59872 Answers: 1 Comments: 0
Question Number 59870 Answers: 2 Comments: 7

Question Number 59861 Answers: 2 Comments: 2
Pg 1509 Pg 1510 Pg 1511 Pg 1512 Pg 1513 Pg 1514 Pg 1515 Pg 1516 Pg 1517 Pg 1518
