
AllQuestion and Answers: Page 1513
Question Number 60498 Answers: 0 Comments: 4
Question Number 60595 Answers: 0 Comments: 2
Question Number 60496 Answers: 0 Comments: 1
Question Number 60495 Answers: 0 Comments: 0
Question Number 60494 Answers: 1 Comments: 1
$${find}\:\int\:\sqrt{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }−{x}}{dx} \\ $$
Question Number 60493 Answers: 0 Comments: 0
Question Number 60484 Answers: 1 Comments: 2
Question Number 60481 Answers: 0 Comments: 0
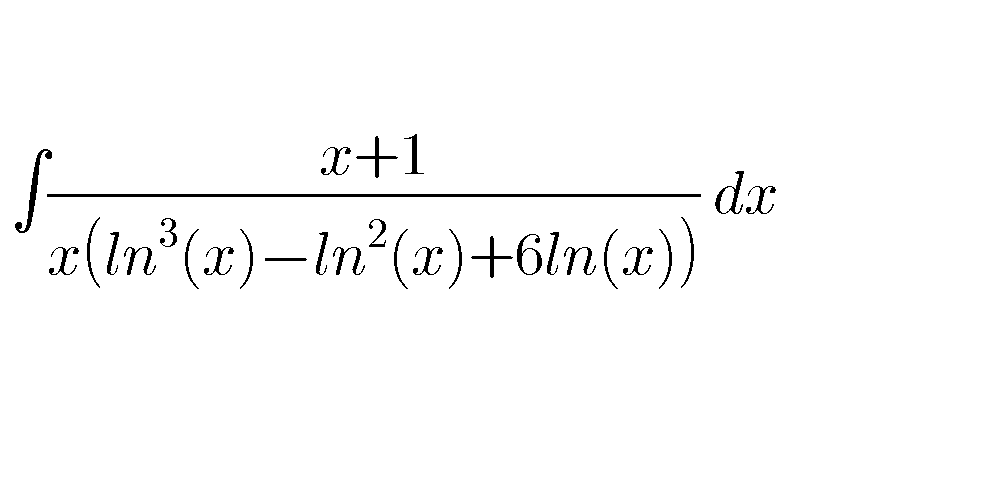
Question Number 60856 Answers: 0 Comments: 0
Question Number 60477 Answers: 2 Comments: 0

Question Number 60475 Answers: 1 Comments: 0

Question Number 60461 Answers: 1 Comments: 0
Question Number 60459 Answers: 0 Comments: 4

Question Number 60453 Answers: 0 Comments: 0

Question Number 60452 Answers: 1 Comments: 1

Question Number 60450 Answers: 0 Comments: 0
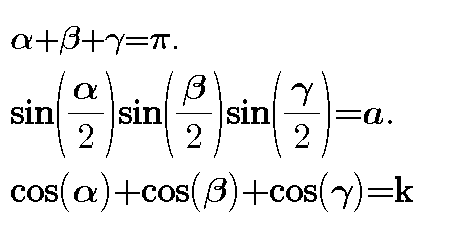
Question Number 60445 Answers: 2 Comments: 1

Question Number 60441 Answers: 1 Comments: 0
Question Number 60426 Answers: 0 Comments: 2
Question Number 60425 Answers: 0 Comments: 0

Question Number 60424 Answers: 0 Comments: 2
Question Number 60423 Answers: 1 Comments: 0

Question Number 60422 Answers: 1 Comments: 5

Question Number 60421 Answers: 1 Comments: 0

Question Number 60416 Answers: 0 Comments: 0
Question Number 60413 Answers: 1 Comments: 4

Pg 1508 Pg 1509 Pg 1510 Pg 1511 Pg 1512 Pg 1513 Pg 1514 Pg 1515 Pg 1516 Pg 1517
