
AllQuestion and Answers: Page 1512
Question Number 60212 Answers: 1 Comments: 1

Question Number 60203 Answers: 2 Comments: 1
Question Number 60202 Answers: 0 Comments: 0
Question Number 60197 Answers: 1 Comments: 1
Question Number 60198 Answers: 1 Comments: 0
Question Number 60189 Answers: 0 Comments: 0
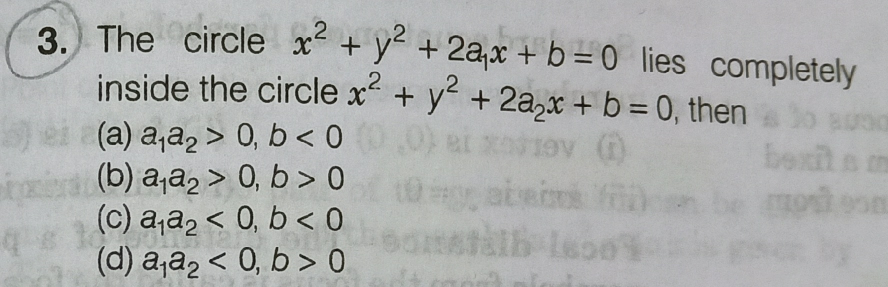
Question Number 60175 Answers: 0 Comments: 2
Question Number 60170 Answers: 0 Comments: 0
Question Number 60156 Answers: 3 Comments: 2
Question Number 60152 Answers: 0 Comments: 16
Question Number 60155 Answers: 1 Comments: 0
Question Number 60143 Answers: 1 Comments: 0
Question Number 60135 Answers: 1 Comments: 0

Question Number 60133 Answers: 2 Comments: 1
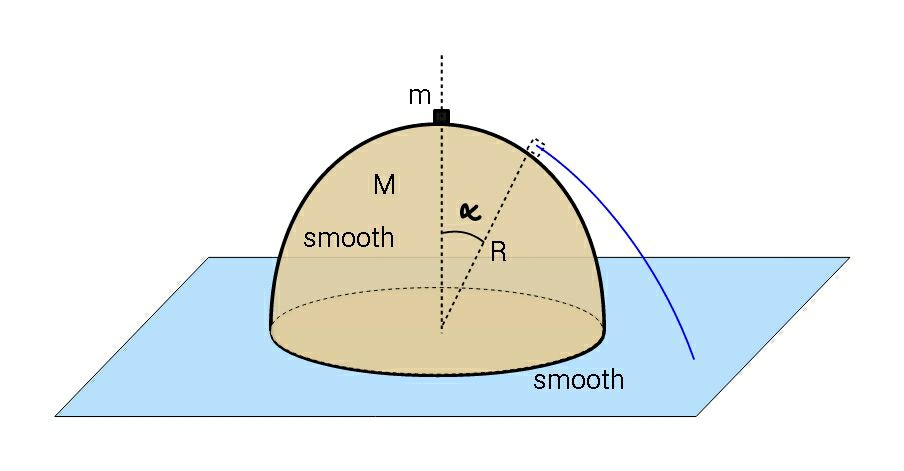
Question Number 60132 Answers: 0 Comments: 1

Question Number 60121 Answers: 2 Comments: 3

Question Number 60115 Answers: 0 Comments: 2

Question Number 60095 Answers: 1 Comments: 1
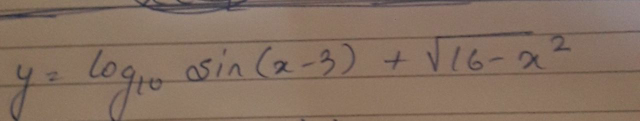
Question Number 60088 Answers: 1 Comments: 1

Question Number 60085 Answers: 1 Comments: 4

Question Number 60058 Answers: 1 Comments: 1

Question Number 60056 Answers: 1 Comments: 1

Question Number 60054 Answers: 1 Comments: 1
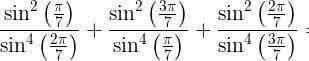
Question Number 60053 Answers: 0 Comments: 0
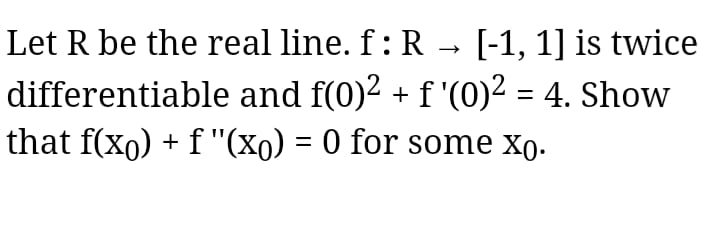
Question Number 60052 Answers: 0 Comments: 0
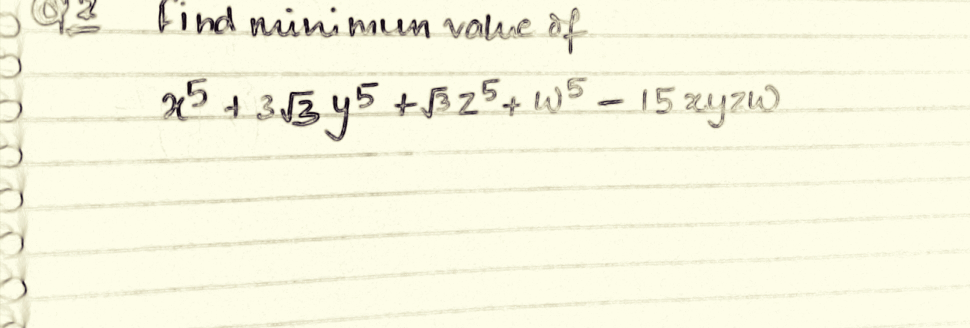
Question Number 60050 Answers: 1 Comments: 1
Pg 1507 Pg 1508 Pg 1509 Pg 1510 Pg 1511 Pg 1512 Pg 1513 Pg 1514 Pg 1515 Pg 1516
