Question and Answers Forum

AllQuestion and Answers: Page 1511

Question Number 58195 Answers: 2 Comments: 0

(1/x)+(1/y)=(3/4) (x^2 /y)+(y^2 /x)=9 find the value of x and y

$$\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{y}}+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{x}}=\mathrm{9} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y} \\ $$

Question Number 58193 Answers: 0 Comments: 0

If z ∈ C such that R(z^n )>0 for n∈N^+ . Show that z ∈R^+ .

$$\mathrm{If}\:{z}\:\in\:\mathbb{C}\:\:\mathrm{such}\:\mathrm{that}\:\mathfrak{R}\left({z}^{{n}} \right)>\mathrm{0}\:\mathrm{for}\:{n}\in\mathbb{N}^{+} . \\ $$$$\mathrm{Show}\:\mathrm{that}\:{z}\:\in\mathbb{R}^{+} . \\ $$

Question Number 58187 Answers: 0 Comments: 0

let f(x) =∫_1 ^3 arctan(x+(x/t))dt withx>0 1) determine a explicit form of f(x) 2) give f^′ (x) at form of integral and find its value 3) calculate ∫_1 ^3 arctan(1+(1/t))dt and ∫_1 ^3 arctan(2+(2/t))dt . 4) calculate ∫_1 ^3 (2t−1)arctan(1+(1/t))dt .

$${let}\:{f}\left({x}\right)\:=\int_{\mathrm{1}} ^{\mathrm{3}} \:{arctan}\left({x}+\frac{{x}}{{t}}\right){dt}\:\:\:{withx}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{determine}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:\:{give}\:{f}^{'} \left({x}\right)\:{at}\:{form}\:{of}\:{integral}\:{and}\:{find}\:{its}\:{value} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\int_{\mathrm{1}} ^{\mathrm{3}} \:{arctan}\left(\mathrm{1}+\frac{\mathrm{1}}{{t}}\right){dt}\:\:\:{and}\:\:\:\:\int_{\mathrm{1}} ^{\mathrm{3}} \:{arctan}\left(\mathrm{2}+\frac{\mathrm{2}}{{t}}\right){dt}\:. \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\left(\mathrm{2}{t}−\mathrm{1}\right){arctan}\left(\mathrm{1}+\frac{\mathrm{1}}{{t}}\right){dt}\:. \\ $$

Question Number 58185 Answers: 0 Comments: 0

find ∫ ((xdx)/(cosx +sin(2x)))

$${find}\:\int\:\:\:\frac{{xdx}}{{cosx}\:+{sin}\left(\mathrm{2}{x}\right)} \\ $$

Question Number 58184 Answers: 0 Comments: 0

find ∫ ((xdx)/(sinx +cos(2x)))

$${find}\:\:\int\:\:\:\:\:\:\frac{{xdx}}{{sinx}\:+{cos}\left(\mathrm{2}{x}\right)} \\ $$

Question Number 58178 Answers: 0 Comments: 0

Question Number 58177 Answers: 2 Comments: 0

cos^(−1) (1/2) + 2 sin^(−1) (1/2) =

$$\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\:+\:\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\:\:= \\ $$

Question Number 58176 Answers: 1 Comments: 0

If x_1 , x_2 , x_3 , x_4 are roots of the equation x^4 −x^3 sin 2β+x^2 cos 2β−x cos β−sin β=0, then tan^(−1) x_1 +tan^(−1) x_2 +tan^(−1) x_3 +tan^(−1) x_4 =

$$\mathrm{If}\:\:{x}_{\mathrm{1}} ,\:{x}_{\mathrm{2}} ,\:{x}_{\mathrm{3}} ,\:{x}_{\mathrm{4}} \:\:\mathrm{are}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$${x}^{\mathrm{4}} −{x}^{\mathrm{3}} \mathrm{sin}\:\mathrm{2}\beta+{x}^{\mathrm{2}} \mathrm{cos}\:\mathrm{2}\beta−{x}\:\mathrm{cos}\:\beta−\mathrm{sin}\:\beta=\mathrm{0}, \\ $$$$\mathrm{then} \\ $$$$\mathrm{tan}^{−\mathrm{1}} {x}_{\mathrm{1}} +\mathrm{tan}^{−\mathrm{1}} {x}_{\mathrm{2}} +\mathrm{tan}^{−\mathrm{1}} {x}_{\mathrm{3}} +\mathrm{tan}^{−\mathrm{1}} {x}_{\mathrm{4}} = \\ $$

Question Number 58175 Answers: 1 Comments: 0

The value of sin(π+θ) sin(π−θ) cosec^2 θ is equal to

$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\mathrm{sin}\left(\pi+\theta\right)\:\mathrm{sin}\left(\pi−\theta\right)\:\mathrm{cosec}^{\mathrm{2}} \theta \\ $$$$\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$

Question Number 58174 Answers: 0 Comments: 2

Four digit integers are taken at random and are multiplied together. Then the probability that only one of them will be alive at the end of the year is

$$\mathrm{Four}\:\mathrm{digit}\:\mathrm{integers}\:\mathrm{are}\:\mathrm{taken}\:\mathrm{at}\:\mathrm{random} \\ $$$$\mathrm{and}\:\mathrm{are}\:\mathrm{multiplied}\:\mathrm{together}.\:\mathrm{Then}\:\mathrm{the} \\ $$$$\mathrm{probability}\:\mathrm{that}\:\mathrm{only}\:\mathrm{one}\:\mathrm{of}\:\mathrm{them}\:\mathrm{will} \\ $$$$\mathrm{be}\:\mathrm{alive}\:\mathrm{at}\:\mathrm{the}\:\mathrm{end}\:\mathrm{of}\:\mathrm{the}\:\mathrm{year}\:\mathrm{is} \\ $$

Question Number 58171 Answers: 1 Comments: 0

a particle of mass m kg is moving along a smooth wire that is fixed in a plane. The polar equation of the wire is r = ae^(3θ) . The particle moves with a cons tant velocity of 6. At time t = 0 , the par ticle is at the point with polar equation (a,θ) a)Find the transverse and radial compo nents of the acceleration of the particle in terms of a and t. b) the resultant force on the particle is F. Show that the magnitude of F at time t is 360mae^(18t)

Question Number 58168 Answers: 2 Comments: 0

find ∫ ((√(tanx))/(sin(2x)))dx

$${find}\:\int\:\:\:\:\frac{\sqrt{{tanx}}}{{sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$

Question Number 58156 Answers: 1 Comments: 0

Jaiden buys 334 cupcakes.He got 14 more cupcakes.How many cupcakes did he got altogether?

$$\mathrm{Jaiden}\:\mathrm{buys}\:\mathrm{334}\:\mathrm{cupcakes}.\mathrm{He}\:\mathrm{got}\:\mathrm{14}\:\mathrm{more}\:\mathrm{cupcakes}.\mathrm{How}\:\mathrm{many}\:\mathrm{cupcakes}\:\mathrm{did}\:\mathrm{he}\:\mathrm{got}\:\mathrm{altogether}? \\ $$

Question Number 58154 Answers: 1 Comments: 0

A(1,1+i),B((√2)+i,2),C(1−3i,1−i) are given. find angle between: AB and AC .

Question Number 58153 Answers: 1 Comments: 0

arctan((√2)−i)=? [i=(√(−1))]

$$\boldsymbol{\mathrm{arctan}}\left(\sqrt{\mathrm{2}}−\boldsymbol{\mathrm{i}}\right)=?\:\:\:\:\:\:\:\:\:\:\left[\boldsymbol{\mathrm{i}}=\sqrt{−\mathrm{1}}\right] \\ $$

Question Number 58145 Answers: 1 Comments: 0

how to factorize a^3 b^2 +a^2 b^3

$${how}\:{to}\:{factorize} \\ $$$${a}^{\mathrm{3}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{3}} \: \\ $$

Question Number 58135 Answers: 1 Comments: 0

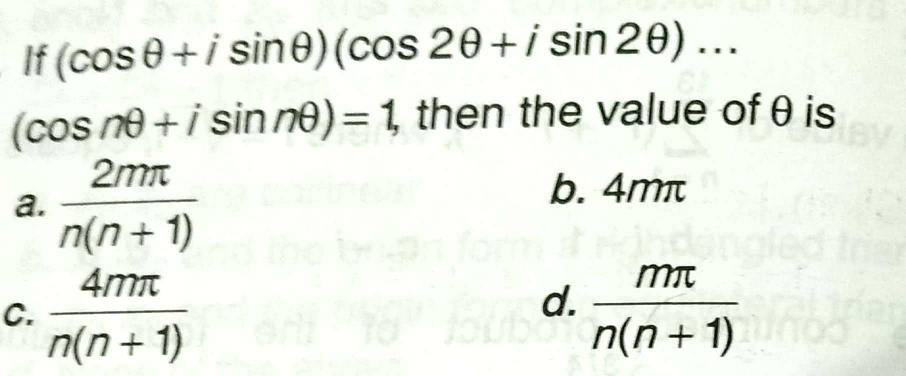
Question Number 58132 Answers: 2 Comments: 1

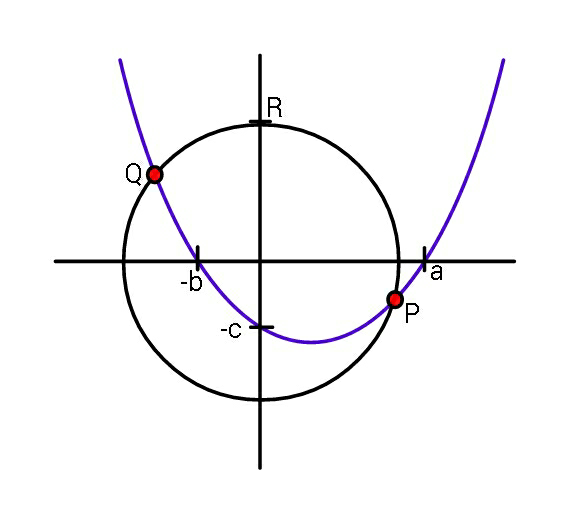
Question Number 58113 Answers: 0 Comments: 1

once sgain: it′s boring to solve questions of minor complexity. we don′t have to, we do it to help unexperienced people to grow. you could at least type “thanks”. otherwise you might be ignored after a while...

$$\mathrm{once}\:\mathrm{sgain}:\:\mathrm{it}'\mathrm{s}\:\mathrm{boring}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{questions}\:\mathrm{of} \\ $$$$\mathrm{minor}\:\mathrm{complexity}.\:\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{to},\:\mathrm{we}\:\mathrm{do} \\ $$$$\mathrm{it}\:\mathrm{to}\:\mathrm{help}\:\mathrm{unexperienced}\:\mathrm{people}\:\mathrm{to}\:\mathrm{grow}. \\ $$$$\mathrm{you}\:\mathrm{could}\:\mathrm{at}\:\mathrm{least}\:\mathrm{type}\:``\mathrm{thanks}''.\:\mathrm{otherwise} \\ $$$$\mathrm{you}\:\mathrm{might}\:\mathrm{be}\:\mathrm{ignored}\:\mathrm{after}\:\mathrm{a}\:\mathrm{while}... \\ $$

Question Number 58103 Answers: 1 Comments: 0

f(x)=−x^6 +3 x^4 + 4x^2 find the zeros

$${f}\left({x}\right)=−{x}^{\mathrm{6}} +\mathrm{3}\:{x}^{\mathrm{4}} \:+\:\mathrm{4}{x}^{\mathrm{2}} {find}\:{the}\:{zeros} \\ $$

Question Number 58097 Answers: 2 Comments: 0

Find the angle between the curves: 1)x^2 y=1−y and x^3 =2−2y. 2) x^2 +y^2 =a^2 (√2) and x^2 −y^2 =a^2 .

$${Find}\:{the}\:{angle}\:{between}\:{the}\:{curves}: \\ $$$$\left.\mathrm{1}\right){x}^{\mathrm{2}} {y}=\mathrm{1}−{y}\:{and}\:{x}^{\mathrm{3}} =\mathrm{2}−\mathrm{2}{y}. \\ $$$$\left.\mathrm{2}\right)\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \sqrt{\mathrm{2}}\:{and}\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} ={a}^{\mathrm{2}} . \\ $$

Question Number 58092 Answers: 3 Comments: 0

6x^3 +5x^2 −6x−5=0

$$\mathrm{6}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{5}=\mathrm{0} \\ $$

Question Number 58091 Answers: 2 Comments: 0

27x^(3−1=0)