
AllQuestion and Answers: Page 1510
Question Number 60783 Answers: 0 Comments: 2
Question Number 60775 Answers: 0 Comments: 1
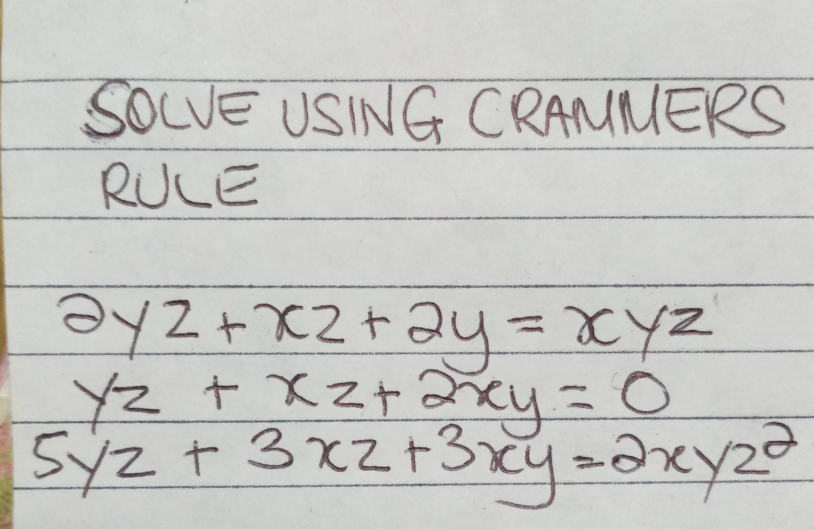
Question Number 60765 Answers: 0 Comments: 2
Question Number 60756 Answers: 1 Comments: 1
Question Number 60748 Answers: 1 Comments: 1

Question Number 60745 Answers: 4 Comments: 5

Question Number 60739 Answers: 1 Comments: 4
Question Number 60735 Answers: 3 Comments: 0
Question Number 60734 Answers: 1 Comments: 4
Question Number 60731 Answers: 0 Comments: 0
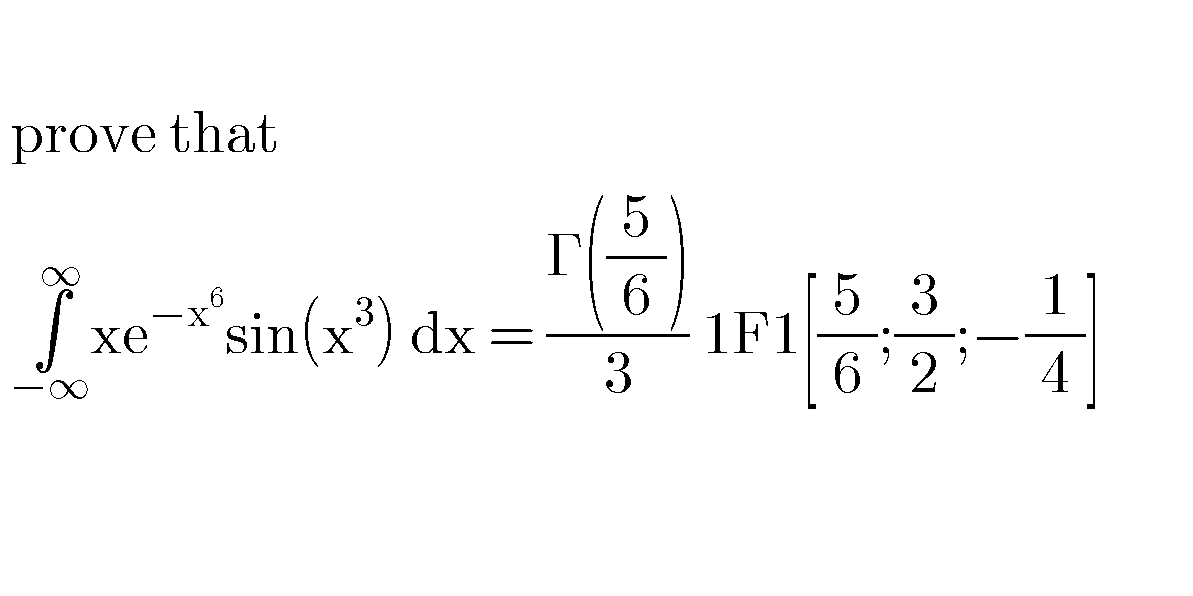
Question Number 60728 Answers: 0 Comments: 0
Question Number 60727 Answers: 0 Comments: 2
Question Number 60725 Answers: 0 Comments: 2
Question Number 60723 Answers: 0 Comments: 10
Question Number 60717 Answers: 0 Comments: 1

Question Number 60706 Answers: 0 Comments: 2
Question Number 60705 Answers: 1 Comments: 0
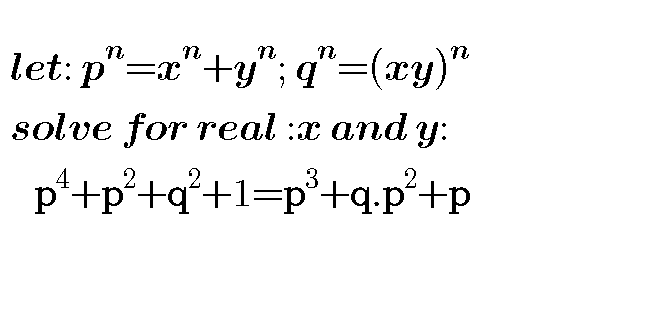
Question Number 60716 Answers: 1 Comments: 1

Question Number 60702 Answers: 0 Comments: 0

Question Number 60701 Answers: 0 Comments: 1
Question Number 60697 Answers: 1 Comments: 1
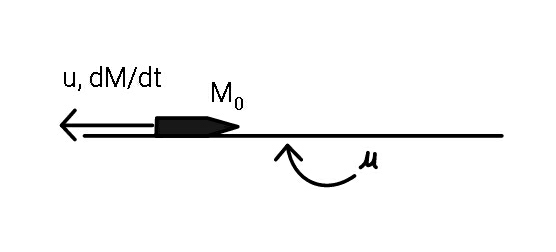
Question Number 60695 Answers: 0 Comments: 1
Question Number 60694 Answers: 0 Comments: 0
Question Number 60693 Answers: 0 Comments: 0
Question Number 60692 Answers: 0 Comments: 0
$${find}\:\:\int\:\:{arctan}\left(\mathrm{2}{cosx}\right){dx}\: \\ $$
Question Number 60691 Answers: 0 Comments: 1
Pg 1505 Pg 1506 Pg 1507 Pg 1508 Pg 1509 Pg 1510 Pg 1511 Pg 1512 Pg 1513 Pg 1514
