
AllQuestion and Answers: Page 1509
Question Number 60948 Answers: 0 Comments: 1
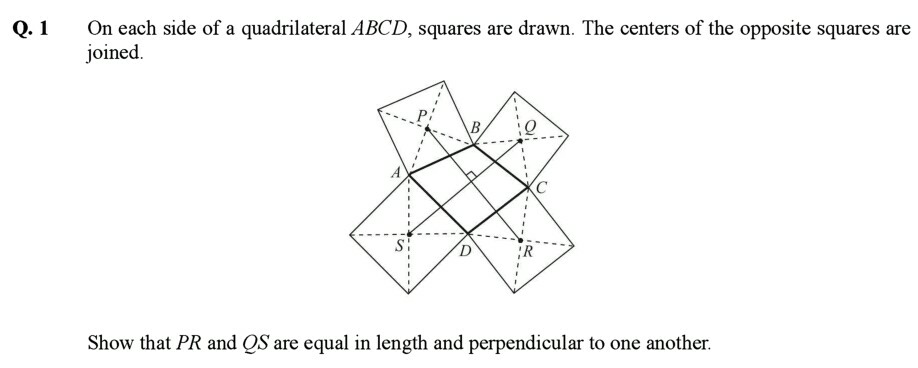
Question Number 60946 Answers: 3 Comments: 4
$$\mathrm{Find}\:\mathrm{x}:\:\:\:\:\:\:\mathrm{x}^{\mathrm{x}} \:\:=\:\:\mathrm{2x} \\ $$
Question Number 60944 Answers: 1 Comments: 1
Question Number 60938 Answers: 0 Comments: 1
Question Number 60921 Answers: 1 Comments: 0
Question Number 60915 Answers: 0 Comments: 0
Question Number 60906 Answers: 0 Comments: 1

Question Number 60905 Answers: 3 Comments: 0
Question Number 60901 Answers: 1 Comments: 0
$${find}\:\int\:\:{arctan}\left(\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx}\: \\ $$
Question Number 60894 Answers: 0 Comments: 0
Question Number 60893 Answers: 1 Comments: 1
Question Number 60910 Answers: 1 Comments: 7
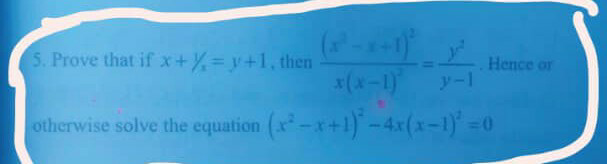
Question Number 60888 Answers: 1 Comments: 1
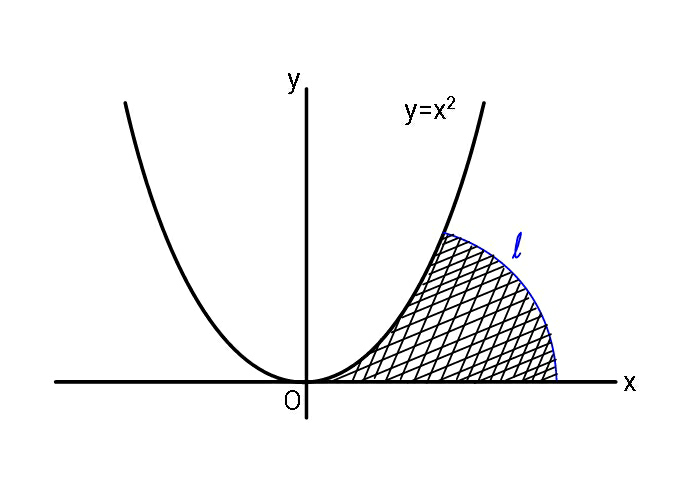
Question Number 60873 Answers: 2 Comments: 5
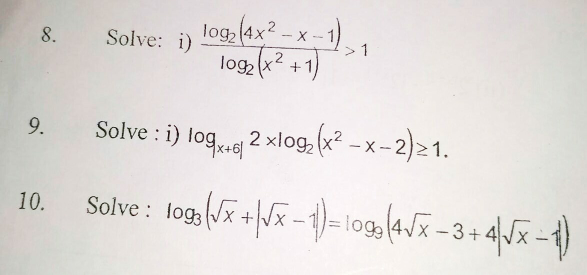
Question Number 60881 Answers: 0 Comments: 3
Question Number 60862 Answers: 0 Comments: 0

Question Number 60854 Answers: 2 Comments: 4
Question Number 60853 Answers: 2 Comments: 0
$$\sqrt{\mathrm{5}−\mathrm{12}{i}}+\sqrt{\mathrm{5}+\mathrm{12}{i}}=? \\ $$
Question Number 60849 Answers: 1 Comments: 5
Question Number 61612 Answers: 0 Comments: 7
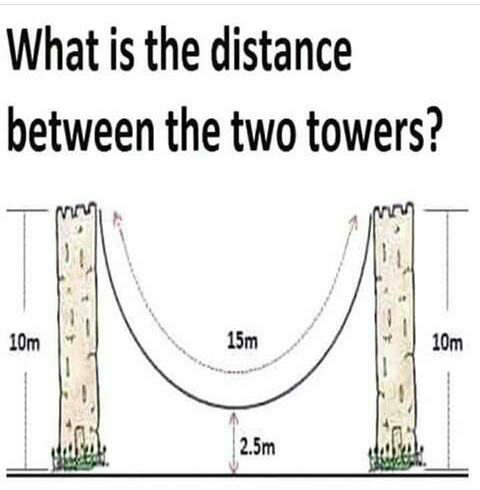
Question Number 60817 Answers: 4 Comments: 2
Question Number 60816 Answers: 1 Comments: 0
Question Number 60814 Answers: 1 Comments: 0
Question Number 60812 Answers: 0 Comments: 5

Question Number 60797 Answers: 0 Comments: 2
$$\int\frac{{e}^{{w}} }{{w}^{{n}+\mathrm{1}} }{dw},\:{n}\in\mathbb{N} \\ $$
Question Number 60791 Answers: 1 Comments: 2
$$\int\frac{{e}^{{n}} }{{x}^{{n}+\mathrm{1}} }{dx},\:\mathrm{n}\in\mathbb{N} \\ $$
Pg 1504 Pg 1505 Pg 1506 Pg 1507 Pg 1508 Pg 1509 Pg 1510 Pg 1511 Pg 1512 Pg 1513
