
AllQuestion and Answers: Page 1508
Question Number 61061 Answers: 1 Comments: 1

Question Number 61056 Answers: 2 Comments: 0
Question Number 61045 Answers: 2 Comments: 2
Question Number 61042 Answers: 1 Comments: 0

Question Number 61041 Answers: 1 Comments: 1
Question Number 61030 Answers: 0 Comments: 2
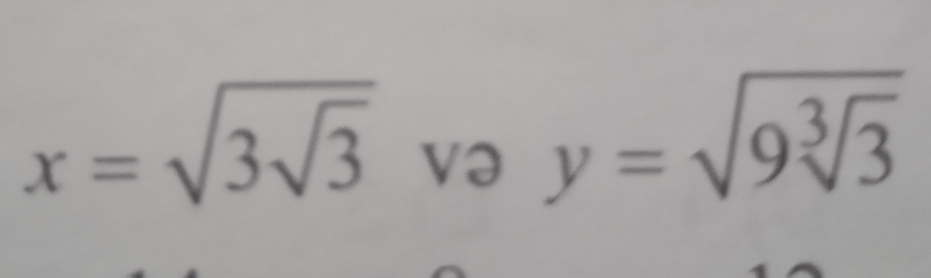
Question Number 61027 Answers: 0 Comments: 3

Question Number 61039 Answers: 0 Comments: 1
Question Number 61048 Answers: 1 Comments: 1
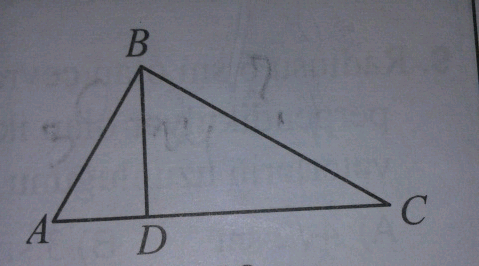
Question Number 61003 Answers: 3 Comments: 0

Question Number 61111 Answers: 1 Comments: 2
Question Number 61202 Answers: 1 Comments: 1

Question Number 61205 Answers: 0 Comments: 4
Question Number 60987 Answers: 1 Comments: 1
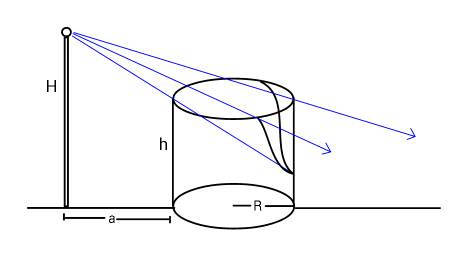
Question Number 60984 Answers: 2 Comments: 9
Question Number 60981 Answers: 2 Comments: 6
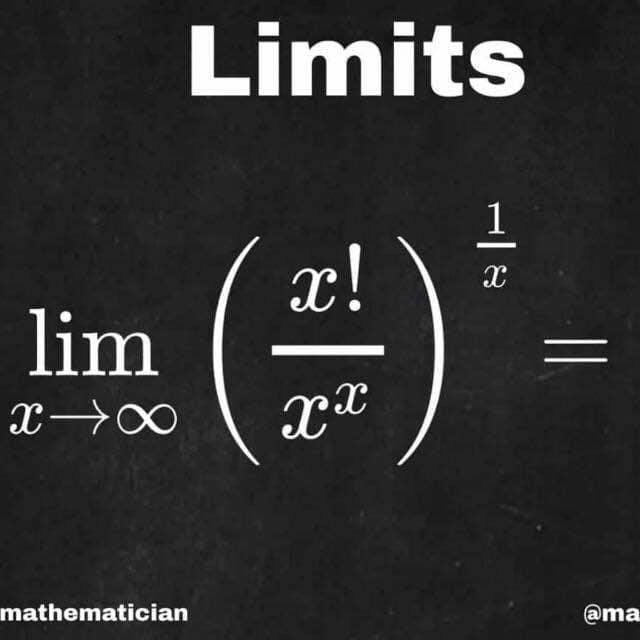
Question Number 60976 Answers: 0 Comments: 1
Question Number 60980 Answers: 1 Comments: 2
Question Number 60967 Answers: 0 Comments: 4
Question Number 60960 Answers: 0 Comments: 2
Question Number 60955 Answers: 1 Comments: 4

Question Number 60948 Answers: 0 Comments: 1
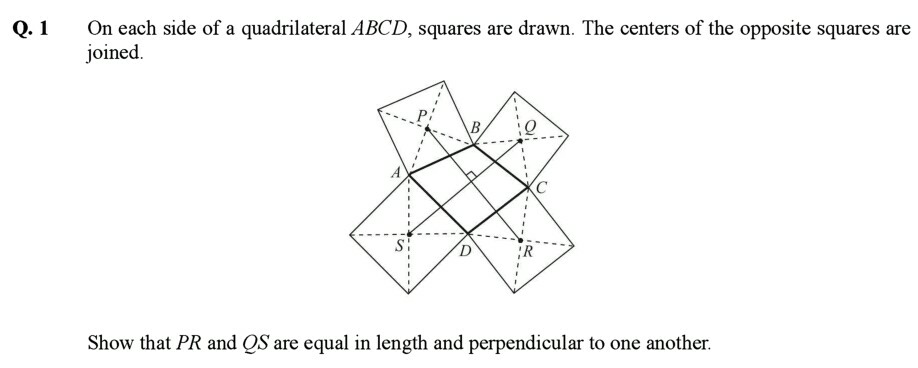
Question Number 60946 Answers: 3 Comments: 4
$$\mathrm{Find}\:\mathrm{x}:\:\:\:\:\:\:\mathrm{x}^{\mathrm{x}} \:\:=\:\:\mathrm{2x} \\ $$
Question Number 60944 Answers: 1 Comments: 1
Question Number 60938 Answers: 0 Comments: 1
Question Number 60921 Answers: 1 Comments: 0
Pg 1503 Pg 1504 Pg 1505 Pg 1506 Pg 1507 Pg 1508 Pg 1509 Pg 1510 Pg 1511 Pg 1512
