Question and Answers Forum

AllQuestion and Answers: Page 1507

Question Number 61241 Answers: 5 Comments: 0

Question Number 61240 Answers: 1 Comments: 3

∫ ((x^(2 ) − 4)/((x^2 + 4)^2 )) dx

$$\int\:\frac{\mathrm{x}^{\mathrm{2}\:} −\:\mathrm{4}}{\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{4}\right)^{\mathrm{2}} }\:\mathrm{dx} \\ $$

Question Number 61237 Answers: 0 Comments: 0

Question Number 61235 Answers: 0 Comments: 6

Question Number 61232 Answers: 0 Comments: 3

let U_n =∫_1 ^(+∞) (([nx]−[(n−1)x])/x^3 ) dx with n≥1 1) find U_n interms of n 2) find lim_(n→+∞) U_n 3) study the serie Σ_(n=1) ^∞ U_n

$${let}\:{U}_{{n}} =\int_{\mathrm{1}} ^{+\infty} \:\:\:\frac{\left[{nx}\right]−\left[\left({n}−\mathrm{1}\right){x}\right]}{{x}^{\mathrm{3}} }\:{dx}\:\:{with}\:{n}\geqslant\mathrm{1} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{U}_{{n}} \:{interms}\:{of}\:{n} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{lim}_{{n}\rightarrow+\infty} \:{U}_{{n}} \\ $$$$\left.\mathrm{3}\right)\:{study}\:{the}\:{serie}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:{U}_{{n}} \\ $$

Question Number 61229 Answers: 1 Comments: 0

let f_n (a) =∫_0 ^a x^n (√(a^2 −x^2 ))dx with a>0 1) determine a explicit form of f(a) 2) let g_n (a) =f^′ (a) give g_n (a) at form of integral and give its value 3) find the value of ∫_0 ^2 x^3 (√(4−x^2 ))dx and ∫_0 ^(√3) x^4 (√(3−x^2 ))dx

$${let}\:{f}_{{n}} \left({a}\right)\:=\int_{\mathrm{0}} ^{{a}} \:{x}^{{n}} \sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}\:\:{with}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{determine}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({a}\right) \\ $$$$\left.\mathrm{2}\right)\:{let}\:{g}_{{n}} \left({a}\right)\:={f}^{'} \left({a}\right)\:\:\:{give}\:{g}_{{n}} \left({a}\right)\:{at}\:{form}\:{of}\:{integral}\:{and}\:{give}\:{its} \\ $$$${value}\: \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{2}} \:{x}^{\mathrm{3}} \sqrt{\mathrm{4}−{x}^{\mathrm{2}} }{dx}\:\:{and}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} {x}^{\mathrm{4}} \sqrt{\mathrm{3}−{x}^{\mathrm{2}} }{dx}\: \\ $$

Question Number 61215 Answers: 2 Comments: 0

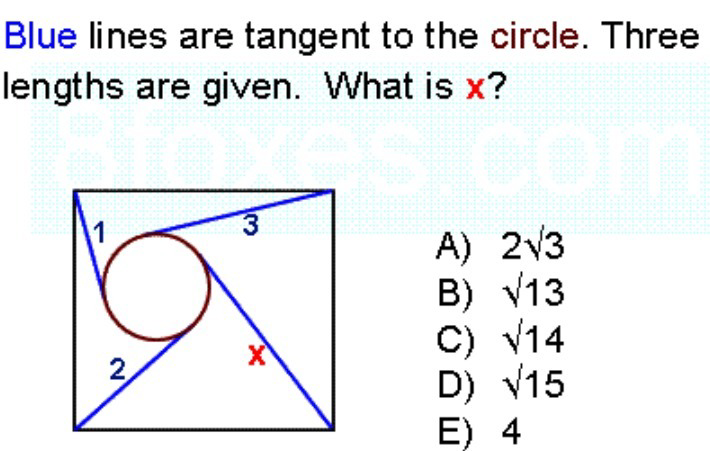
Question Number 61208 Answers: 0 Comments: 8

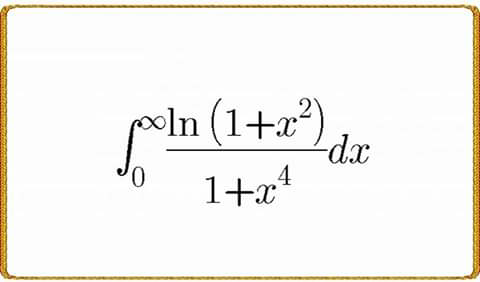
Question Number 61211 Answers: 1 Comments: 3

Solve for x in terms of a (√(a−(√(a+x )))) + (√(a+(√(a−x)))) = 2x Please sir i request you to solve this question =_=

$${Solve}\:{for}\:{x}\:{in}\:{terms}\:{of}\:{a}\: \\ $$$$\sqrt{{a}−\sqrt{{a}+{x}\:}}\:+\:\:\sqrt{{a}+\sqrt{{a}−{x}}}\:=\:\mathrm{2}{x} \\ $$$${Please}\:{sir}\:{i}\:{request}\:{you}\:{to}\:{solve}\:{this}\: \\ $$$${question}\:=\_= \\ $$

Question Number 61210 Answers: 2 Comments: 1

for what value of θ, e^(iθ) =0

$${for}\:{what}\:{value}\:{of}\:\theta,\:\:{e}^{{i}\theta} =\mathrm{0}\:\: \\ $$

Question Number 61180 Answers: 1 Comments: 0

solve y^(′′) +3y^′ −y =sin(2x)

$${solve}\:{y}^{''} \:+\mathrm{3}{y}^{'} −{y}\:={sin}\left(\mathrm{2}{x}\right) \\ $$

Question Number 61181 Answers: 0 Comments: 0

sove (1+e^(−x) )y^(′′) +(2+e^x )y^′ =(x+1)e^x

$${sove}\:\left(\mathrm{1}+{e}^{−{x}} \right){y}^{''} \:+\left(\mathrm{2}+{e}^{{x}} \right){y}^{'} \:=\left({x}+\mathrm{1}\right){e}^{{x}} \\ $$

Question Number 61169 Answers: 1 Comments: 1

Question Number 61165 Answers: 1 Comments: 0

Question Number 61162 Answers: 1 Comments: 3

if sin(x) = ((x − 20)/(20)) , find x

$$\mathrm{if}\:\:\:\:\:\mathrm{sin}\left(\mathrm{x}\right)\:\:=\:\:\frac{\mathrm{x}\:−\:\mathrm{20}}{\mathrm{20}}\:\:,\:\:\:\mathrm{find}\:\:\mathrm{x} \\ $$

Question Number 61157 Answers: 1 Comments: 3

if tan 5θ + tan 4θ =1 find 3θ

$${if} \\ $$$${tan}\:\mathrm{5}\theta\:+\:{tan}\:\mathrm{4}\theta\:=\mathrm{1} \\ $$$${find}\:\mathrm{3}\theta \\ $$$$ \\ $$$$ \\ $$

Question Number 61151 Answers: 0 Comments: 0

Question Number 61147 Answers: 1 Comments: 0

prove ∫((1+cos x)/(1−cos x))dx=−2cot (x/2)−x+c

$$\boldsymbol{{prove}} \\ $$$$\int\frac{\mathrm{1}+{cos}\:{x}}{\mathrm{1}−{cos}\:{x}}{dx}=−\mathrm{2}{cot}\:\frac{{x}}{\mathrm{2}}−{x}+{c} \\ $$$$ \\ $$

Question Number 61142 Answers: 0 Comments: 0

Question Number 61140 Answers: 1 Comments: 1

can we find an exact solution? t^6 +4t^4 −12t^3 +24t^2 −24t+8=0

$$\mathrm{can}\:\mathrm{we}\:\mathrm{find}\:\mathrm{an}\:\mathrm{exact}\:\mathrm{solution}? \\ $$$${t}^{\mathrm{6}} +\mathrm{4}{t}^{\mathrm{4}} −\mathrm{12}{t}^{\mathrm{3}} +\mathrm{24}{t}^{\mathrm{2}} −\mathrm{24}{t}+\mathrm{8}=\mathrm{0} \\ $$

Question Number 61137 Answers: 1 Comments: 0

What is the sum of first 3n term of an AP , if the sunm of first n term is 2n and sum of first 2n term is 5n

$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{first}\:\mathrm{3n}\:\mathrm{term}\:\mathrm{of}\:\mathrm{an}\:\mathrm{AP}\:,\:\mathrm{if}\:\mathrm{the}\:\mathrm{sunm}\:\mathrm{of}\:\mathrm{first}\:\mathrm{n}\:\mathrm{term}\:\mathrm{is} \\ $$$$\mathrm{2n}\:\:\mathrm{and}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{first}\:\mathrm{2n}\:\mathrm{term}\:\mathrm{is}\:\:\mathrm{5n} \\ $$

Question Number 61117 Answers: 2 Comments: 0

The 2nd, 4th and 8th term of an AP are the consecutive term of a GP. If the sum of the 3rd and 4th term of the AP is 20. Find the sum of the first four terms of the AP.

$$\mathrm{The}\:\mathrm{2nd},\:\mathrm{4th}\:\mathrm{and}\:\mathrm{8th}\:\mathrm{term}\:\mathrm{of}\:\mathrm{an}\:\mathrm{AP}\:\mathrm{are}\:\mathrm{the}\:\mathrm{consecutive}\:\mathrm{term}\:\mathrm{of}\:\mathrm{a}\:\mathrm{GP}. \\ $$$$\mathrm{If}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{3rd}\:\mathrm{and}\:\mathrm{4th}\:\mathrm{term}\:\mathrm{of}\:\mathrm{the}\:\mathrm{AP}\:\mathrm{is}\:\mathrm{20}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{first}\:\mathrm{four}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{AP}. \\ $$

Question Number 61116 Answers: 1 Comments: 0

Question Number 61186 Answers: 0 Comments: 3

Question Number 61112 Answers: 2 Comments: 4

Question Number 61107 Answers: 0 Comments: 0

solve Cauchy′s problem x′= t + (((μx)^2 )/(1+(μx)^2 )), μ∈R x(0)=0

$${solve}\:{Cauchy}'{s}\:{problem} \\ $$$${x}'=\:{t}\:+\:\frac{\left(\mu{x}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\mu{x}\right)^{\mathrm{2}} },\:\mu\in\mathbb{R} \\ $$$${x}\left(\mathrm{0}\right)=\mathrm{0} \\ $$

Pg 1502 Pg 1503 Pg 1504 Pg 1505 Pg 1506 Pg 1507 Pg 1508 Pg 1509 Pg 1510 Pg 1511

Contact: [email protected]