
AllQuestion and Answers: Page 1506
Question Number 61335 Answers: 1 Comments: 0
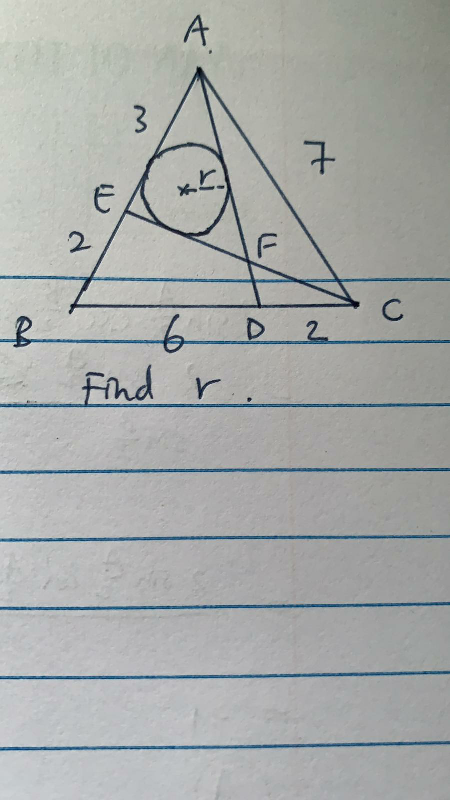
Question Number 61329 Answers: 0 Comments: 2
Question Number 61328 Answers: 0 Comments: 4
Question Number 61327 Answers: 1 Comments: 0

Question Number 61326 Answers: 0 Comments: 4
Question Number 61322 Answers: 1 Comments: 0

Question Number 61320 Answers: 1 Comments: 0
Question Number 61318 Answers: 1 Comments: 0

Question Number 61313 Answers: 0 Comments: 3
Question Number 61303 Answers: 2 Comments: 3

Question Number 61297 Answers: 0 Comments: 0
Question Number 61284 Answers: 0 Comments: 0
Question Number 61283 Answers: 1 Comments: 0
Question Number 61274 Answers: 1 Comments: 0
Question Number 61272 Answers: 0 Comments: 0

Question Number 61273 Answers: 2 Comments: 2
Question Number 61270 Answers: 2 Comments: 0

Question Number 61269 Answers: 3 Comments: 0
Question Number 61268 Answers: 0 Comments: 0
Question Number 61267 Answers: 0 Comments: 0
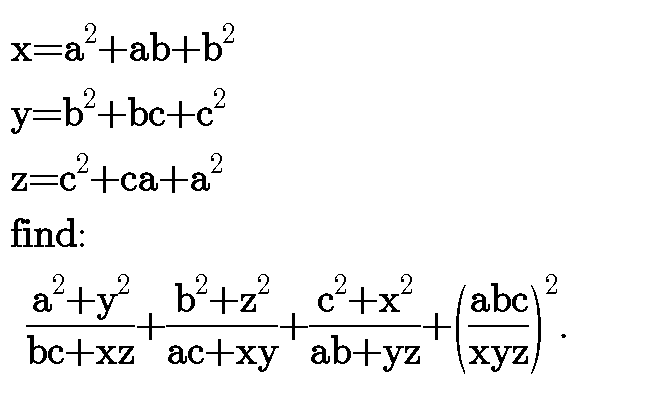
Question Number 61261 Answers: 1 Comments: 0
Question Number 61258 Answers: 1 Comments: 2
Question Number 61241 Answers: 5 Comments: 0

Question Number 61240 Answers: 1 Comments: 3
Question Number 61237 Answers: 0 Comments: 0

Question Number 61235 Answers: 0 Comments: 6

Pg 1501 Pg 1502 Pg 1503 Pg 1504 Pg 1505 Pg 1506 Pg 1507 Pg 1508 Pg 1509 Pg 1510
