
AllQuestion and Answers: Page 1503
Question Number 61751 Answers: 0 Comments: 0
Question Number 61750 Answers: 0 Comments: 0
Question Number 61749 Answers: 0 Comments: 0
$${find}\:\int\:\:\frac{{dx}}{{cos}\left(\mathrm{2}{x}\right)+{tan}\left({x}\right)} \\ $$
Question Number 61744 Answers: 0 Comments: 7
Question Number 61738 Answers: 2 Comments: 0

Question Number 61735 Answers: 0 Comments: 0
Question Number 61733 Answers: 0 Comments: 1
Question Number 61721 Answers: 0 Comments: 0
Question Number 61719 Answers: 0 Comments: 1
Question Number 61708 Answers: 0 Comments: 1
$$\mathrm{8}+\left(\mathrm{4}+\mathrm{3}×\mathrm{2}\right) \\ $$
Question Number 61707 Answers: 0 Comments: 1
Question Number 61706 Answers: 0 Comments: 1
$$\frac{\mathrm{7}^{\mathrm{10}} }{\mathrm{7}^{\mathrm{7}} } \\ $$
Question Number 61694 Answers: 1 Comments: 1
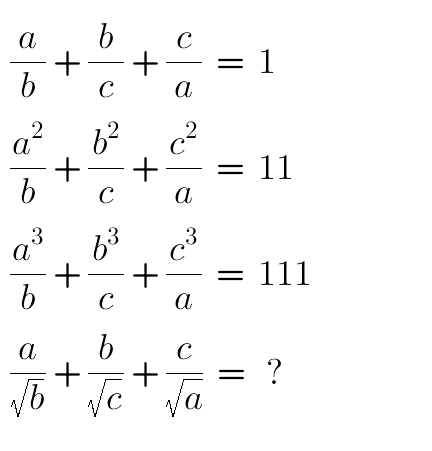
Question Number 61692 Answers: 0 Comments: 0
Question Number 61691 Answers: 0 Comments: 0
Question Number 61700 Answers: 1 Comments: 0

Question Number 61724 Answers: 0 Comments: 6
$$\underset{{n}\geqslant\mathrm{0}} {\sum}{n}^{\mathrm{2}} {x}^{{n}} \\ $$$$ \\ $$
Question Number 61662 Answers: 0 Comments: 1
Question Number 61661 Answers: 0 Comments: 1
Question Number 61660 Answers: 0 Comments: 1
Question Number 61657 Answers: 0 Comments: 0
Question Number 61675 Answers: 1 Comments: 1
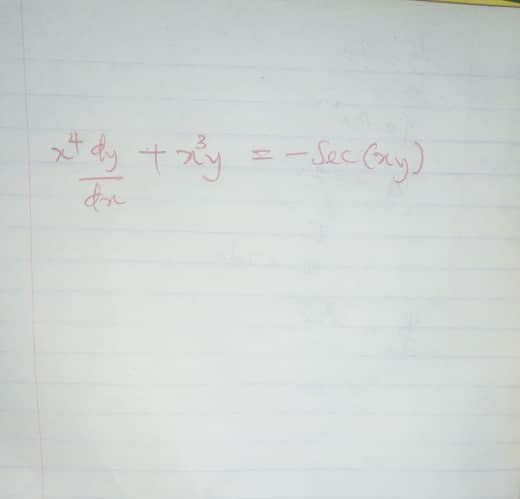
Question Number 61674 Answers: 1 Comments: 4
Question Number 61654 Answers: 0 Comments: 0
Question Number 61646 Answers: 0 Comments: 0
Question Number 61645 Answers: 0 Comments: 1
Pg 1498 Pg 1499 Pg 1500 Pg 1501 Pg 1502 Pg 1503 Pg 1504 Pg 1505 Pg 1506 Pg 1507
