
AllQuestion and Answers: Page 1500
Question Number 62034 Answers: 0 Comments: 0
Question Number 62024 Answers: 0 Comments: 0

Question Number 62023 Answers: 3 Comments: 3
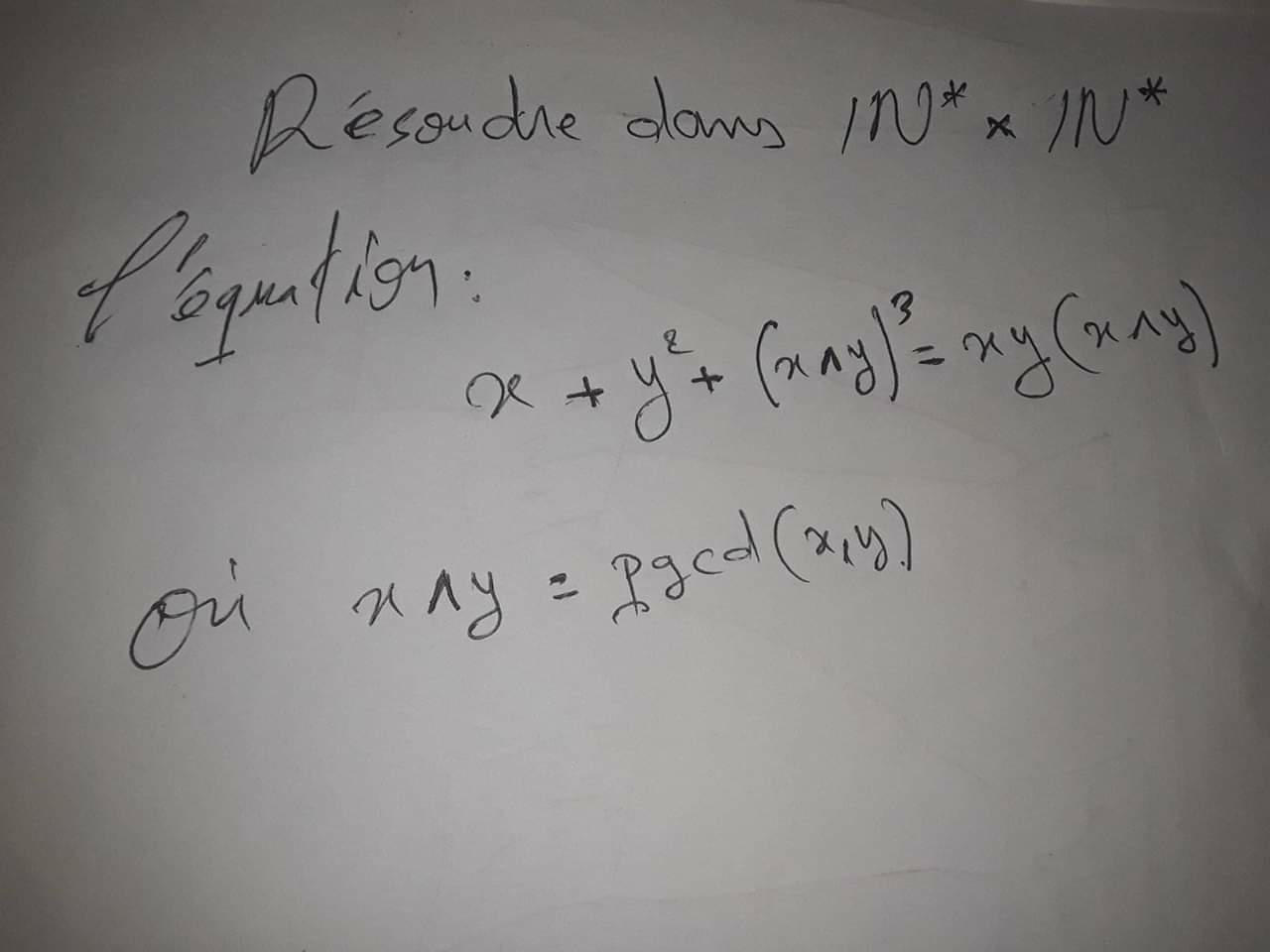
Question Number 62022 Answers: 1 Comments: 0

Question Number 62019 Answers: 0 Comments: 1

Question Number 62016 Answers: 0 Comments: 1
Question Number 62014 Answers: 1 Comments: 0

Question Number 62010 Answers: 0 Comments: 0
Question Number 62003 Answers: 0 Comments: 0
Question Number 62002 Answers: 0 Comments: 0
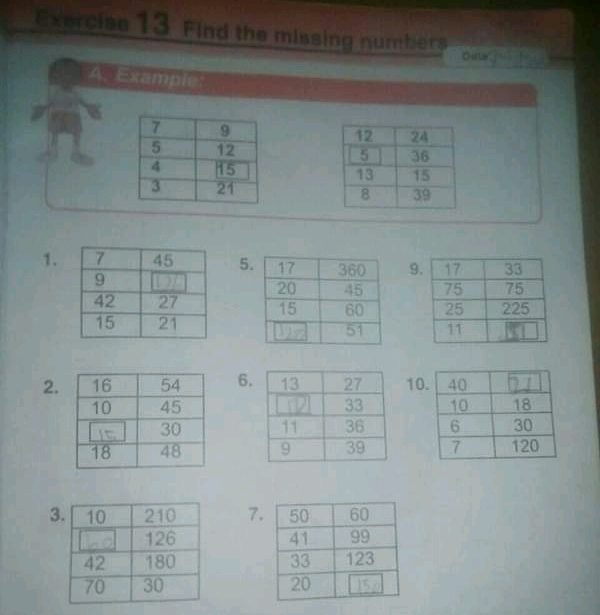
Question Number 62001 Answers: 0 Comments: 1
Question Number 62000 Answers: 0 Comments: 0
Question Number 61994 Answers: 1 Comments: 1

Question Number 61993 Answers: 1 Comments: 0
Question Number 62046 Answers: 0 Comments: 1
$$\mathrm{4}×\left(\mathrm{3}+\mathrm{2}−\mathrm{3}\right) \\ $$
Question Number 61981 Answers: 0 Comments: 1
Question Number 61979 Answers: 0 Comments: 1
Question Number 61978 Answers: 0 Comments: 5
Question Number 61976 Answers: 0 Comments: 2
Question Number 61966 Answers: 2 Comments: 4
$$\int\frac{\mathrm{1}}{{e}^{\mathrm{2}{x}} −{e}^{−\mathrm{2}{x}} }\:{dx} \\ $$
Question Number 61954 Answers: 0 Comments: 1

Question Number 61952 Answers: 1 Comments: 1

Question Number 61948 Answers: 0 Comments: 0
Question Number 61938 Answers: 0 Comments: 0

Question Number 61937 Answers: 1 Comments: 5
Question Number 61934 Answers: 1 Comments: 2
Pg 1495 Pg 1496 Pg 1497 Pg 1498 Pg 1499 Pg 1500 Pg 1501 Pg 1502 Pg 1503 Pg 1504
