Question and Answers Forum

AllQuestion and Answers: Page 1490

Question Number 62213 Answers: 0 Comments: 1

calculate ∫∫∫_D e^(−x^2 −y^2 ) (√(x^2 +y^2 +z^2 ))dxdydz with D ={(x,y,z)∈R^3 / 0≤x≤1 , 1≤y≤2 and 2≤z≤3 }

$${calculate}\:\int\int\int_{{D}} \:{e}^{−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } \sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:+{z}^{\mathrm{2}} }{dxdydz}\:{with} \\ $$$${D}\:=\left\{\left({x},{y},{z}\right)\in{R}^{\mathrm{3}} \:/\:\:\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:,\:\mathrm{1}\leqslant{y}\leqslant\mathrm{2}\:\:{and}\:\:\:\mathrm{2}\leqslant{z}\leqslant\mathrm{3}\:\right\} \\ $$

Question Number 62211 Answers: 0 Comments: 3

(x/((√(4−x^2 ))+3))Max=(5/3)?

$$\frac{{x}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }+\mathrm{3}}{Max}=\frac{\mathrm{5}}{\mathrm{3}}? \\ $$

Question Number 62210 Answers: 0 Comments: 2

let f(x) =(x+1)^n arctan(nx) calculate f^((n)) (0).

$${let}\:{f}\left({x}\right)\:=\left({x}+\mathrm{1}\right)^{{n}} \:{arctan}\left({nx}\right) \\ $$$${calculate}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right). \\ $$

Question Number 62209 Answers: 1 Comments: 1

find g(a) =∫(x+a)(√(x^2 −a^2 ))dx

$${find}\:{g}\left({a}\right)\:=\int\left({x}+{a}\right)\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{dx}\: \\ $$

Question Number 62208 Answers: 1 Comments: 2

find f(a) =∫ (x−a)(√(x^2 +a^2 ))dx

$${find}\:{f}\left({a}\right)\:=\int\:\:\left({x}−{a}\right)\sqrt{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }{dx} \\ $$

Question Number 62207 Answers: 1 Comments: 1

calculate ∫ ((x+3)/((x−2)(√(x^2 +x+1)))) dx

$${calculate}\:\int\:\:\:\:\:\:\frac{{x}+\mathrm{3}}{\left({x}−\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}\:{dx} \\ $$

Question Number 62206 Answers: 0 Comments: 0

study the convergence of Σ_(n≥0) (−1)^n {[(√(n^2 +2))]−[(√(n^2 +1))])

$${study}\:{the}\:{convergence}\:{of}\:\sum_{{n}\geqslant\mathrm{0}} \:\left(−\mathrm{1}\right)^{{n}} \left\{\left[\sqrt{{n}^{\mathrm{2}} +\mathrm{2}}\right]−\left[\sqrt{{n}^{\mathrm{2}} \:+\mathrm{1}}\right]\right) \\ $$

Question Number 62205 Answers: 0 Comments: 0

study the convergence of Σ_(n≥1) n^2 arctan(1+e^(−n) )

$${study}\:{the}\:{convergence}\:{of}\:\:\sum_{{n}\geqslant\mathrm{1}} \:\:\:{n}^{\mathrm{2}} \:{arctan}\left(\mathrm{1}+{e}^{−{n}} \right) \\ $$

Question Number 62204 Answers: 0 Comments: 1

study the convergence of Σ_(n≥1) ((ln(1+e^(−n^2 ) ))/n^n )

$${study}\:{the}\:{convergence}\:{of}\:\:\:\:\sum_{{n}\geqslant\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{e}^{−{n}^{\mathrm{2}} } \right)}{{n}^{{n}} } \\ $$

Question Number 62203 Answers: 0 Comments: 1

calculate ∫∫_([0,2]^2 ) ((arctan((√(x^2 +y^2 ))))/(3−(√(x^2 +y^2 ))))dxdy

$${calculate}\:\int\int_{\left[\mathrm{0},\mathrm{2}\right]^{\mathrm{2}} } \:\:\:\:\frac{{arctan}\left(\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right)}{\mathrm{3}−\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}{dxdy} \\ $$

Question Number 62202 Answers: 0 Comments: 0

study the convergence of Σ_(n≥1) (((√(n+1))−(√n))/(nln(n+1)))

$${study}\:{the}\:{convergence}\:{of}\:\sum_{{n}\geqslant\mathrm{1}} \:\frac{\sqrt{{n}+\mathrm{1}}−\sqrt{{n}}}{{nln}\left({n}+\mathrm{1}\right)} \\ $$

Question Number 62201 Answers: 0 Comments: 1

calculate ∫∫_W e^(x−2y) sin(x+2y) dxdy W ={(x,y)^2 / 0≤x≤1 and 2≤y≤(√5)}

$${calculate}\:\int\int_{{W}} \:\:{e}^{{x}−\mathrm{2}{y}} {sin}\left({x}+\mathrm{2}{y}\right)\:{dxdy} \\ $$$${W}\:=\left\{\left({x},{y}\right)^{\mathrm{2}} /\:\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:\:{and}\:\:\mathrm{2}\leqslant{y}\leqslant\sqrt{\mathrm{5}}\right\} \\ $$

Question Number 62200 Answers: 1 Comments: 1

calculate lim_(x→0) ((ln(1+x+sinx)−ln(1+sin(2x)))/x^2 )

$${calculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{ln}\left(\mathrm{1}+{x}+{sinx}\right)−{ln}\left(\mathrm{1}+{sin}\left(\mathrm{2}{x}\right)\right)}{{x}^{\mathrm{2}} } \\ $$

Question Number 62199 Answers: 0 Comments: 0

let f(x) =e^(−(1/x)) determine f^((n)) by relation of recurrence .

$${let}\:{f}\left({x}\right)\:={e}^{−\frac{\mathrm{1}}{{x}}} \:\:\:\:\:{determine}\:{f}^{\left({n}\right)} \:{by}\:{relation}\:{of}\:{recurrence}\:. \\ $$

Question Number 62198 Answers: 0 Comments: 0

find ∫∫_([0,1]) ((x^2 −y^2 )/(3−(√(x^2 +y^2 )))) dxdy .

$${find}\:\int\int_{\left[\mathrm{0},\mathrm{1}\right]} \:\:\:\:\frac{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{\mathrm{3}−\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\:{dxdy}\:. \\ $$

Question Number 62197 Answers: 0 Comments: 1

calculate ∫∫_([0,1]^2 ) (√(x^2 +y^2 ))sin((√(x^2 +y^2 )))dxdy

$${calculate}\:\int\int_{\left[\mathrm{0},\mathrm{1}\right]^{\mathrm{2}} } \:\:\:\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{sin}\left(\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right){dxdy} \\ $$

Question Number 62196 Answers: 0 Comments: 1

calculate ∫_0 ^∞ ((ln(2+e^(−t^2 ) ))/(t^2 +3))dt

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left(\mathrm{2}+{e}^{−{t}^{\mathrm{2}} } \right)}{{t}^{\mathrm{2}} \:+\mathrm{3}}{dt} \\ $$

Question Number 62195 Answers: 0 Comments: 0

calculate A_n =∫_(−∞) ^(+∞) (dx/((x^2 +x+1)^n )) with n integr natural(n≥1)

$${calculate}\:\:{A}_{{n}} =\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)^{{n}} }\:\:\:{with}\:{n}\:{integr}\:{natural}\left({n}\geqslant\mathrm{1}\right) \\ $$

Question Number 62192 Answers: 1 Comments: 0

Question Number 62186 Answers: 0 Comments: 0

∫(e^(3x^2 ) /((1−x^4 ))^(1/8) ) dx

$$\int\frac{{e}^{\mathrm{3}{x}^{\mathrm{2}} } }{\sqrt[{\mathrm{8}}]{\mathrm{1}−{x}^{\mathrm{4}} }}\:{dx} \\ $$

Question Number 62185 Answers: 1 Comments: 0

∫(dx/(sin3x+sin4x))

$$\int\frac{{dx}}{{sin}\mathrm{3}{x}+{sin}\mathrm{4}{x}} \\ $$

Question Number 62184 Answers: 0 Comments: 1

((2x−1))^(1/3) + (√(3x+1)) = 3(x)^(1/4)

$$\sqrt[{\mathrm{3}}]{\mathrm{2}{x}−\mathrm{1}}\:+\:\sqrt{\mathrm{3}{x}+\mathrm{1}}\:=\:\mathrm{3}\sqrt[{\mathrm{4}}]{{x}} \\ $$

Question Number 62180 Answers: 0 Comments: 5

lim_(x→∞) ((senx)/x)

$$\underset{{x}\rightarrow\infty} {{lim}}\:\frac{{senx}}{{x}} \\ $$

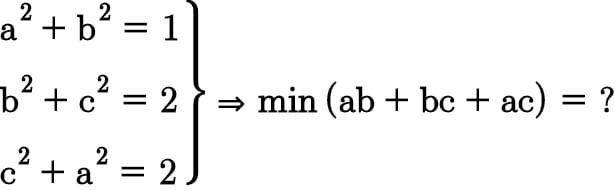
Question Number 62179 Answers: 0 Comments: 1

∫_( 0) ^( 2 (√(ln 3))) ∫_( (y/2)) ^( (√(ln 3))) e^x^2 dx dy

$$\int_{\:\:\mathrm{0}} ^{\:\mathrm{2}\:\sqrt{\mathrm{ln}\:\mathrm{3}}} \:\int_{\:\:\frac{\mathrm{y}}{\mathrm{2}}} ^{\:\sqrt{\mathrm{ln}\:\mathrm{3}}} \:\:\:\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \:\:\mathrm{dx}\:\mathrm{dy} \\ $$

Question Number 62176 Answers: 2 Comments: 0

Question Number 62169 Answers: 1 Comments: 0

Prove without induction that: (1 + (√2))^(2n) + (1 − (√2))^(2n) is even for every natural number n.

$$\mathrm{Prove}\:\mathrm{without}\:\mathrm{induction}\:\mathrm{that}:\:\:\left(\mathrm{1}\:+\:\sqrt{\mathrm{2}}\right)^{\mathrm{2n}} \:+\:\left(\mathrm{1}\:−\:\sqrt{\mathrm{2}}\right)^{\mathrm{2n}} \:\:\mathrm{is}\:\mathrm{even}\:\mathrm{for}\:\mathrm{every} \\ $$$$\mathrm{natural}\:\mathrm{number}\:\mathrm{n}.\:\:\: \\ $$

Pg 1485 Pg 1486 Pg 1487 Pg 1488 Pg 1489 Pg 1490 Pg 1491 Pg 1492 Pg 1493 Pg 1494

Contact: info@tinkutara.com