
AllQuestion and Answers: Page 1488
Question Number 63290 Answers: 0 Comments: 0
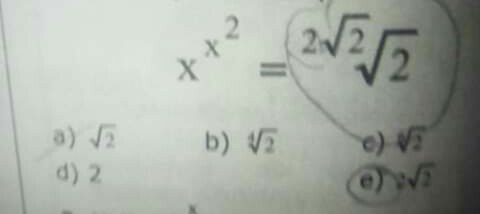
Question Number 63289 Answers: 0 Comments: 0
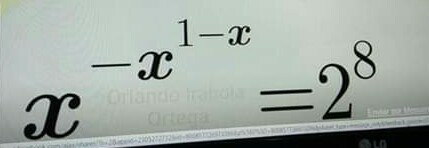
Question Number 63288 Answers: 1 Comments: 0

Question Number 63218 Answers: 0 Comments: 8
Question Number 63178 Answers: 2 Comments: 1
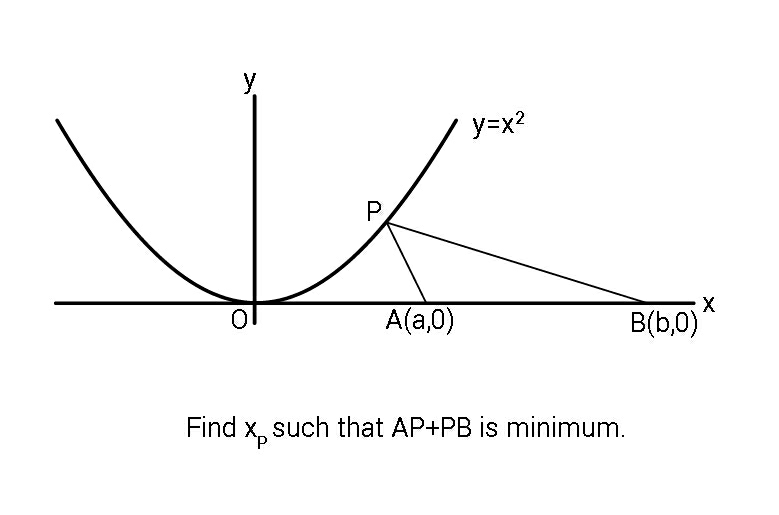
Question Number 63176 Answers: 1 Comments: 1

Question Number 63651 Answers: 0 Comments: 0
Question Number 63175 Answers: 0 Comments: 2
Question Number 63165 Answers: 0 Comments: 0
Question Number 63164 Answers: 0 Comments: 0
Question Number 63162 Answers: 1 Comments: 3
Question Number 63154 Answers: 0 Comments: 5
Question Number 63152 Answers: 0 Comments: 0
Question Number 63143 Answers: 0 Comments: 0

Question Number 63139 Answers: 0 Comments: 3
Question Number 63137 Answers: 1 Comments: 0
Question Number 63128 Answers: 0 Comments: 7
Question Number 63124 Answers: 1 Comments: 5
Question Number 63121 Answers: 0 Comments: 3
Question Number 63120 Answers: 0 Comments: 0
Question Number 63117 Answers: 1 Comments: 1
Question Number 63116 Answers: 1 Comments: 1
$$\int\frac{\mathrm{1}+×}{\sqrt{\mathrm{1}+×^{\mathrm{2}} }}{dx} \\ $$
Question Number 63108 Answers: 2 Comments: 1
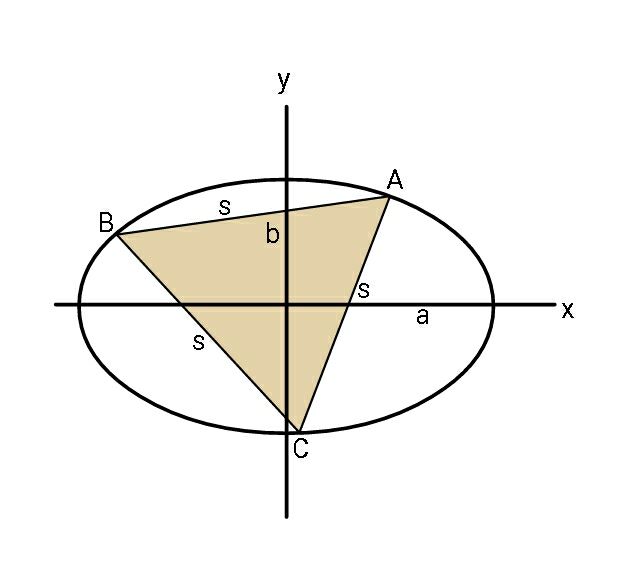
Question Number 63103 Answers: 1 Comments: 2

Question Number 63101 Answers: 3 Comments: 1
Question Number 63095 Answers: 1 Comments: 0

Pg 1483 Pg 1484 Pg 1485 Pg 1486 Pg 1487 Pg 1488 Pg 1489 Pg 1490 Pg 1491 Pg 1492
