
AllQuestion and Answers: Page 1486
Question Number 63427 Answers: 0 Comments: 4
Question Number 63426 Answers: 1 Comments: 5
Question Number 63425 Answers: 0 Comments: 0
Question Number 63424 Answers: 0 Comments: 0
Question Number 63423 Answers: 0 Comments: 1
Question Number 63579 Answers: 0 Comments: 4
Question Number 63410 Answers: 2 Comments: 2
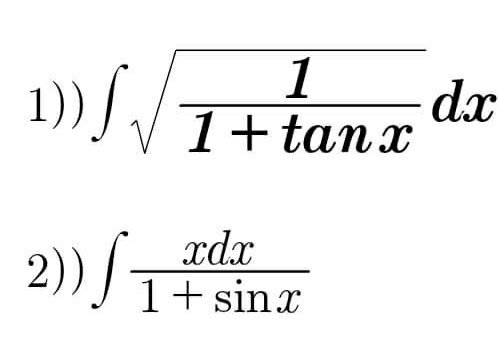
Question Number 63405 Answers: 0 Comments: 0
$${find}\:\int\:\sqrt{\frac{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}}{{x}+\mathrm{2}}}{dx} \\ $$
Question Number 63404 Answers: 1 Comments: 2
Question Number 63407 Answers: 0 Comments: 0
Question Number 63395 Answers: 0 Comments: 3
Question Number 63614 Answers: 0 Comments: 0
Question Number 63389 Answers: 0 Comments: 2
Question Number 63383 Answers: 1 Comments: 1
Question Number 63381 Answers: 0 Comments: 2
Question Number 63378 Answers: 1 Comments: 0
Question Number 63363 Answers: 1 Comments: 3

Question Number 63361 Answers: 0 Comments: 3

Question Number 63351 Answers: 3 Comments: 2
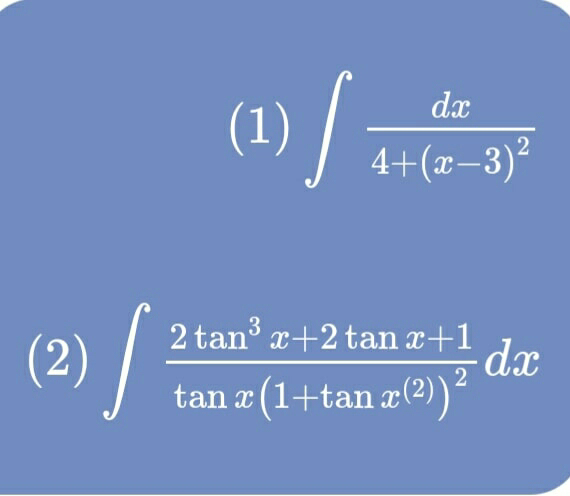
Question Number 63372 Answers: 1 Comments: 2
Question Number 63373 Answers: 0 Comments: 2
Question Number 63336 Answers: 2 Comments: 1

Question Number 63324 Answers: 1 Comments: 0

Question Number 63399 Answers: 1 Comments: 1
Question Number 63301 Answers: 1 Comments: 9
$${find}\:\frac{{dy}}{{dx}}\:{if}\:\:{x}\left({x}\:+{y}\right)\:=\:{y}^{\mathrm{2}} \\ $$
Question Number 63300 Answers: 0 Comments: 2
Pg 1481 Pg 1482 Pg 1483 Pg 1484 Pg 1485 Pg 1486 Pg 1487 Pg 1488 Pg 1489 Pg 1490
