
AllQuestion and Answers: Page 1484
Question Number 63678 Answers: 0 Comments: 1

Question Number 63674 Answers: 0 Comments: 2
Question Number 63667 Answers: 0 Comments: 3
Question Number 63666 Answers: 0 Comments: 3
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{dx}}{\mathrm{2}{sinx}\:+{cosx}} \\ $$
Question Number 63665 Answers: 0 Comments: 1
Question Number 63664 Answers: 0 Comments: 6
Question Number 63663 Answers: 1 Comments: 0
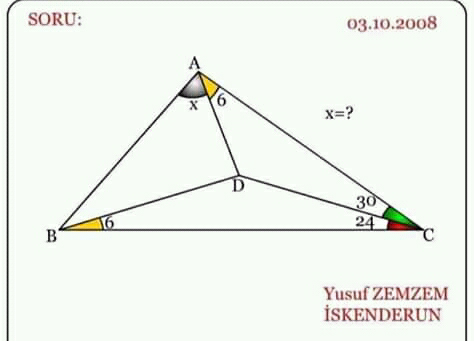
Question Number 63662 Answers: 0 Comments: 1
Question Number 63661 Answers: 0 Comments: 1
Question Number 63642 Answers: 2 Comments: 1
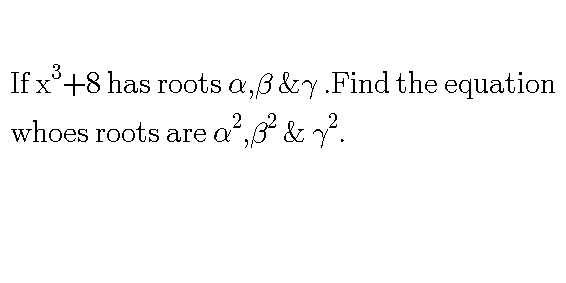
Question Number 63641 Answers: 0 Comments: 2
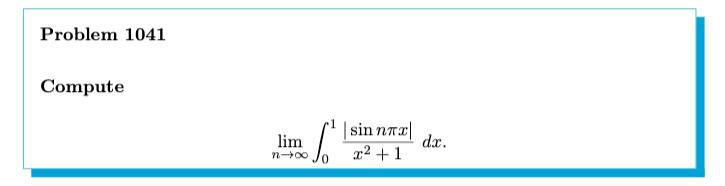
Question Number 63639 Answers: 0 Comments: 0

Question Number 63636 Answers: 0 Comments: 0
Question Number 63618 Answers: 1 Comments: 5

Question Number 63615 Answers: 0 Comments: 5
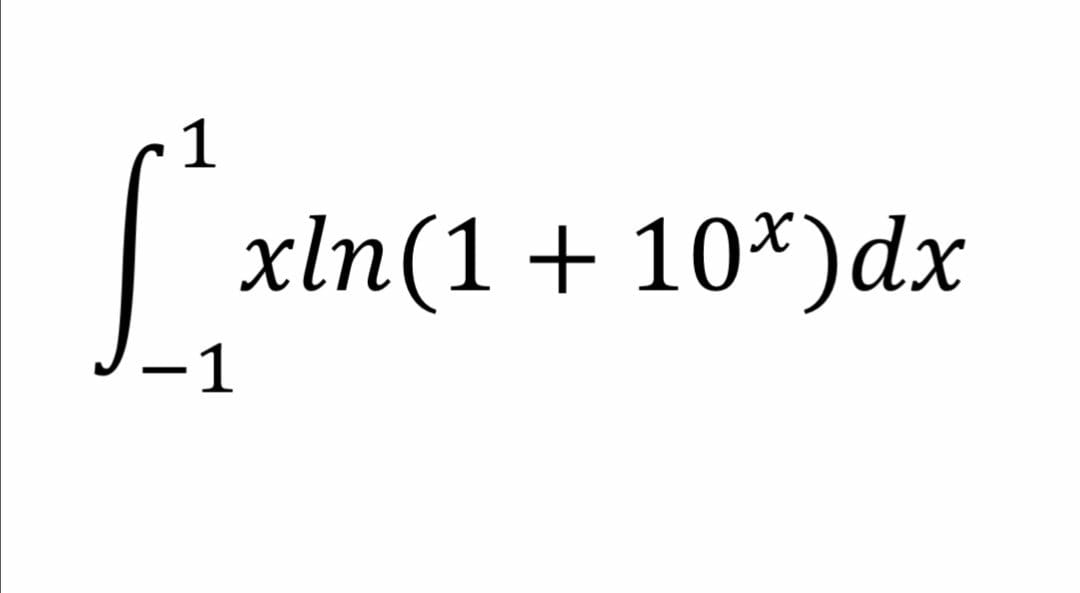
Question Number 63643 Answers: 1 Comments: 0
Question Number 63602 Answers: 2 Comments: 0
Question Number 63597 Answers: 0 Comments: 0

Question Number 63596 Answers: 0 Comments: 1
Question Number 63588 Answers: 1 Comments: 1
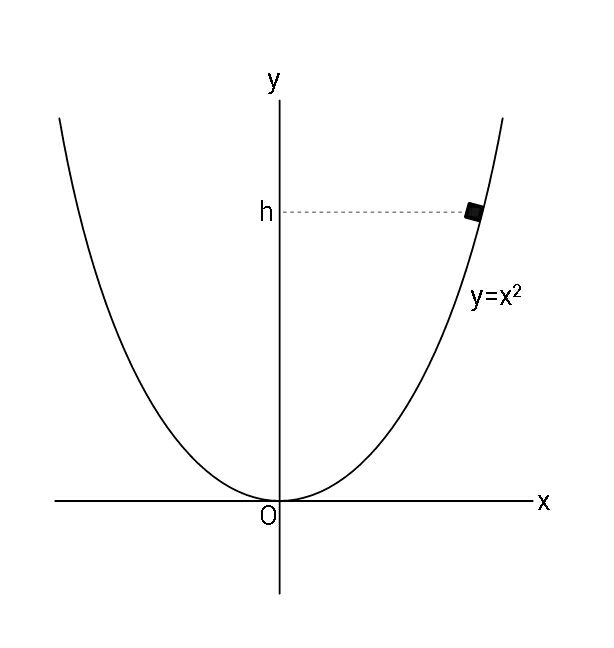
Question Number 63574 Answers: 0 Comments: 12
Question Number 63573 Answers: 0 Comments: 0
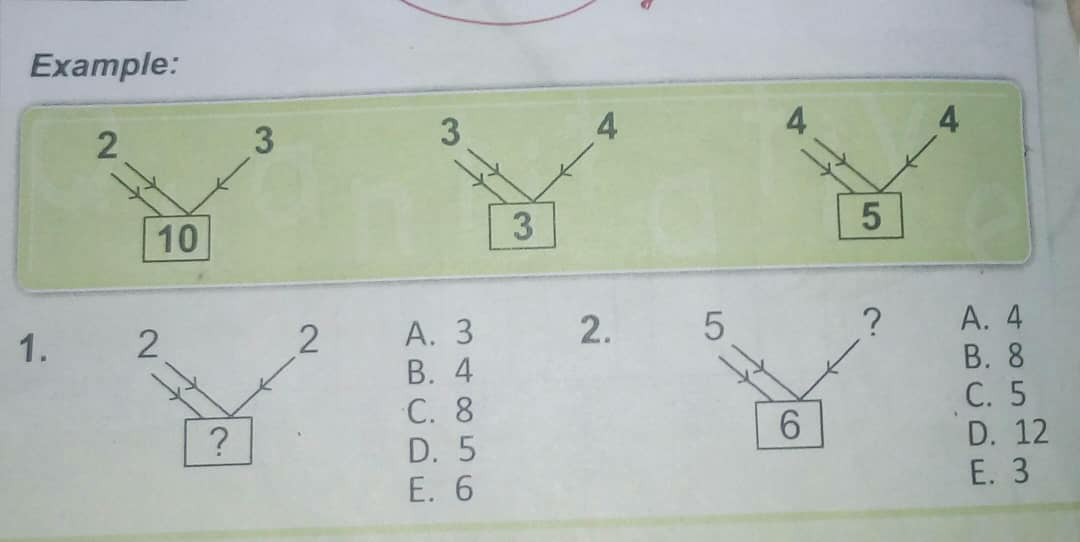
Question Number 63570 Answers: 1 Comments: 3

Question Number 63566 Answers: 0 Comments: 2
Question Number 63565 Answers: 0 Comments: 0
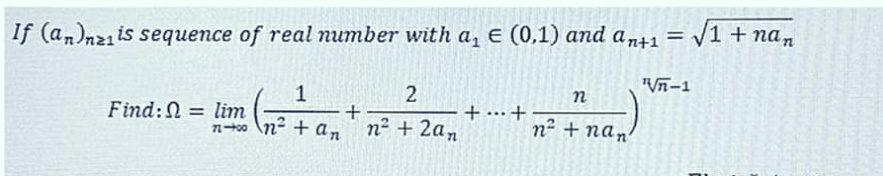
Question Number 63564 Answers: 1 Comments: 0
Pg 1479 Pg 1480 Pg 1481 Pg 1482 Pg 1483 Pg 1484 Pg 1485 Pg 1486 Pg 1487 Pg 1488
