
AllQuestion and Answers: Page 1479
Question Number 63758 Answers: 0 Comments: 6
$$\mathrm{Tanmay}\:\mathrm{Sir}.\:\mathrm{Are}\:\mathrm{you}\:\mathrm{ok}\:? \\ $$
Question Number 63751 Answers: 0 Comments: 0
$$\mathrm{Where}\:\mathrm{is}\:\mathrm{sir}\:\mathrm{tanmay} \\ $$
Question Number 63790 Answers: 2 Comments: 0

Question Number 63789 Answers: 0 Comments: 0

Question Number 63788 Answers: 1 Comments: 0

Question Number 63750 Answers: 1 Comments: 2

Question Number 63748 Answers: 0 Comments: 0
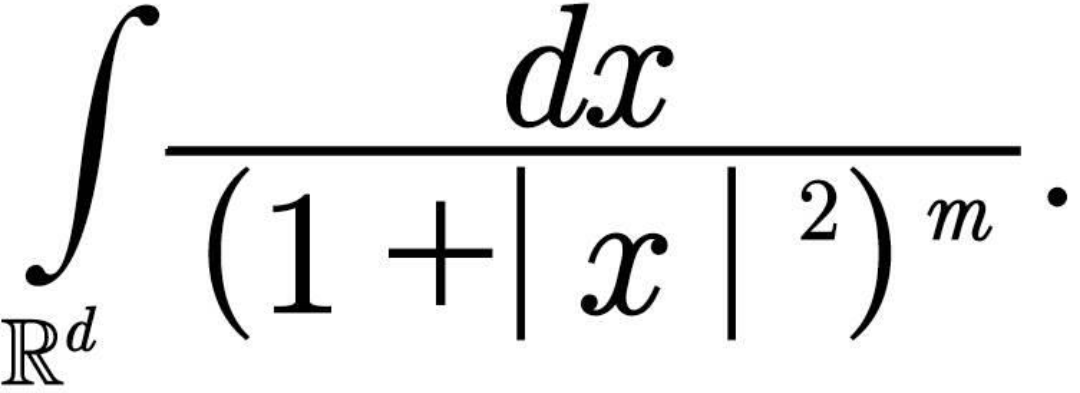
Question Number 63747 Answers: 0 Comments: 1
Question Number 63792 Answers: 0 Comments: 0
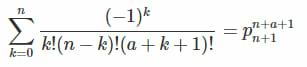
Question Number 63738 Answers: 0 Comments: 0
Question Number 63722 Answers: 1 Comments: 6
Question Number 63721 Answers: 1 Comments: 2
Question Number 63720 Answers: 1 Comments: 2
$${calculate}\:\int\sqrt{\left({x}−\mathrm{3}\right)\left(\mathrm{2}−{x}\right)}{dx} \\ $$
Question Number 63711 Answers: 1 Comments: 1
Question Number 63710 Answers: 0 Comments: 1

Question Number 63703 Answers: 1 Comments: 2
Question Number 63700 Answers: 0 Comments: 0

Question Number 63698 Answers: 0 Comments: 0

Question Number 63693 Answers: 1 Comments: 2
Question Number 63689 Answers: 0 Comments: 3
$${Show}\:{that}\:\:{if}\:\:{a}\mid{b}\:\:{then}\:{an}\mid{bn} \\ $$
Question Number 63684 Answers: 0 Comments: 0
Question Number 63682 Answers: 0 Comments: 0
Question Number 63678 Answers: 0 Comments: 1

Question Number 63674 Answers: 0 Comments: 2
Question Number 63667 Answers: 0 Comments: 3
Question Number 63666 Answers: 0 Comments: 3
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{dx}}{\mathrm{2}{sinx}\:+{cosx}} \\ $$
Pg 1474 Pg 1475 Pg 1476 Pg 1477 Pg 1478 Pg 1479 Pg 1480 Pg 1481 Pg 1482 Pg 1483
