Question and Answers Forum

AllQuestion and Answers: Page 1477

Question Number 64328 Answers: 0 Comments: 0

Let f : R→R, g : R→R be continuous functions. Then ∫_(−π/2) ^(π/2) [ f(x)+f(−x) ] [ g(x)(g(−x) ] dx =

$$\mathrm{Let}\:\:{f}\::\:{R}\rightarrow{R},\:{g}\::\:{R}\rightarrow{R}\:\:\mathrm{be}\:\mathrm{continuous} \\ $$$$\mathrm{functions}.\:\mathrm{Then} \\ $$$$\underset{−\pi/\mathrm{2}} {\overset{\pi/\mathrm{2}} {\int}}\:\left[\:{f}\left({x}\right)+{f}\left(−{x}\right)\:\right]\:\left[\:{g}\left({x}\right)\left({g}\left(−{x}\right)\:\right]\:{dx}\:=\right. \\ $$

Question Number 64327 Answers: 0 Comments: 1

(d/dx) ( ∫_(f(x)) ^(g(x)) φ(t) dt ) =

$$\frac{{d}}{{dx}}\:\:\left(\:\underset{{f}\left({x}\right)} {\overset{{g}\left({x}\right)} {\int}}\:\phi\left({t}\right)\:{dt}\:\right)\:= \\ $$

Question Number 64320 Answers: 1 Comments: 1

without beta function ∫cos^3 t sin^2 t dt

$${without}\:{beta}\:{function} \\ $$$$\int{cos}^{\mathrm{3}} {t}\:{sin}^{\mathrm{2}} {t}\:{dt}\: \\ $$

Question Number 64311 Answers: 3 Comments: 1

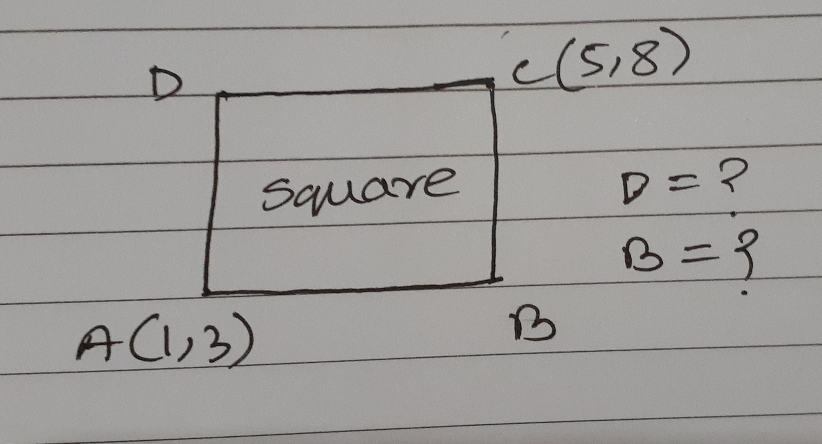
Question Number 64309 Answers: 0 Comments: 1

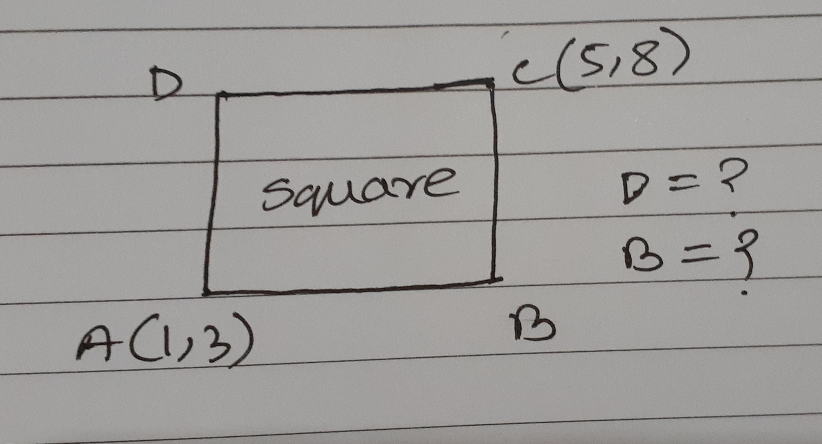
Question Number 64305 Answers: 0 Comments: 6

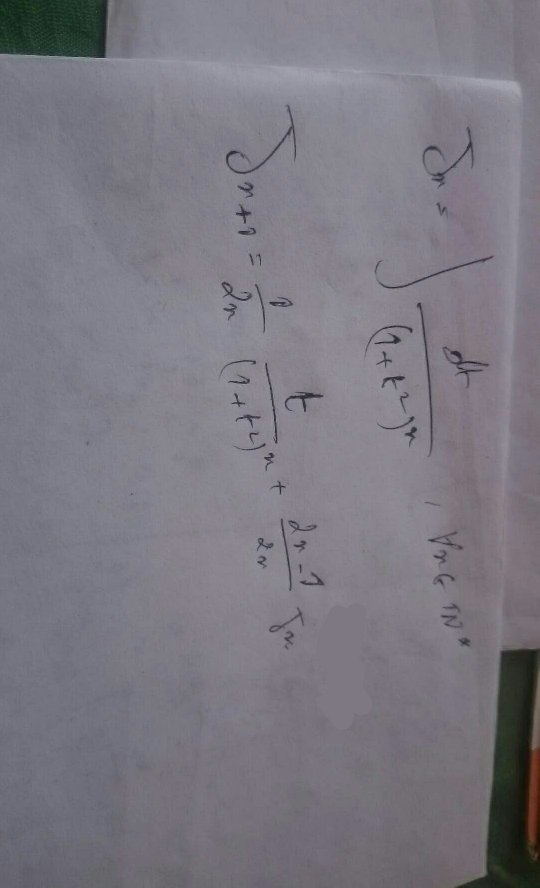
Question Number 64302 Answers: 0 Comments: 0

Question Number 64300 Answers: 0 Comments: 0

Question Number 64299 Answers: 0 Comments: 0

Question Number 64297 Answers: 0 Comments: 0

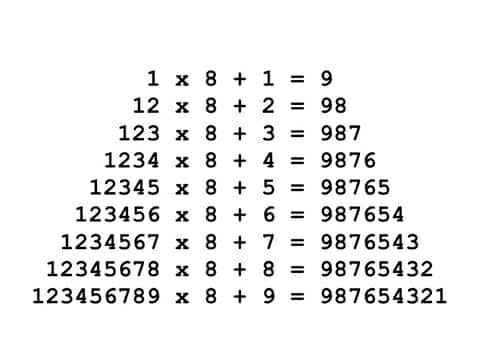
Question Number 64295 Answers: 0 Comments: 0

Question Number 64289 Answers: 2 Comments: 2

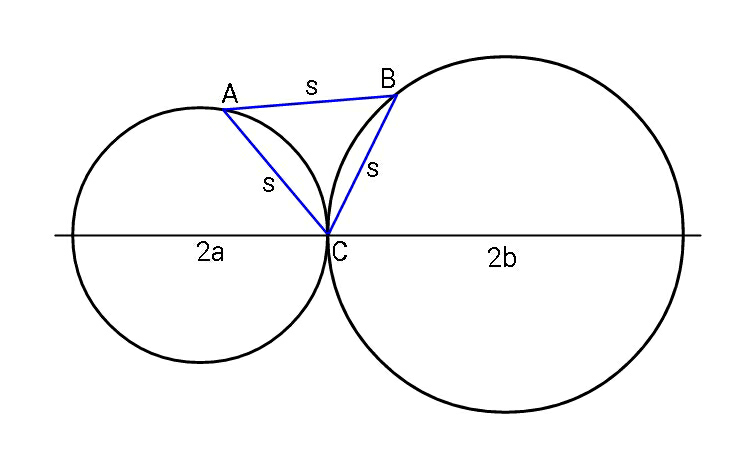
Question Number 64287 Answers: 0 Comments: 3

Question Number 64284 Answers: 0 Comments: 0

Find all the integer solution 3x^2 + 1 = 4y^3

$$\mathrm{Find}\:\mathrm{all}\:\mathrm{the}\:\mathrm{integer}\:\mathrm{solution}\:\:\:\:\:\:\:\mathrm{3x}^{\mathrm{2}} \:+\:\mathrm{1}\:\:=\:\:\mathrm{4y}^{\mathrm{3}} \\ $$

Question Number 64253 Answers: 0 Comments: 1

Question Number 64251 Answers: 0 Comments: 0

Question Number 64250 Answers: 0 Comments: 0

Question Number 64246 Answers: 3 Comments: 0

Question Number 64240 Answers: 1 Comments: 0

Question Number 64238 Answers: 0 Comments: 2

∫ln(x−5)/x^2 +110x−5dx

$$\int{ln}\left({x}−\mathrm{5}\right)/{x}^{\mathrm{2}} +\mathrm{110}{x}−\mathrm{5}{dx} \\ $$

Question Number 64227 Answers: 1 Comments: 0

∫(1/(x^6 +x^3 ))dx=?

$$\int\frac{\mathrm{1}}{{x}^{\mathrm{6}} +{x}^{\mathrm{3}} }{dx}=? \\ $$

Question Number 64225 Answers: 1 Comments: 0

Solution of the equation ∫_(√2) ^x (dx/(x (√(x^2 −1)))) = (π/(12)) is x = _____.

$$\mathrm{Solution}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\underset{\sqrt{\mathrm{2}}} {\overset{{x}} {\int}}\:\:\:\frac{{dx}}{{x}\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:=\:\frac{\pi}{\mathrm{12}}\:\:\mathrm{is}\:\:{x}\:=\:\_\_\_\_\_. \\ $$

Question Number 64224 Answers: 0 Comments: 1

∫x_x dx ∫x^x dx

$$\int{x}_{{x}} {dx} \\ $$$$ \\ $$$$\int{x}^{{x}} {dx} \\ $$

Question Number 64213 Answers: 0 Comments: 2

∫(1/(x!))dx=?

$$\int\frac{\mathrm{1}}{{x}!}{dx}=? \\ $$

Question Number 64267 Answers: 1 Comments: 1

If ∫_( 0) ^π (1/(a+b cos x)) dx, a>0 is equal to (π/(√(a^2 −b^2 ))) , then ∫_( 0) ^π (1/((a+b cos x)^2 )) dx =

$$\mathrm{If}\:\underset{\:\mathrm{0}} {\overset{\pi} {\int}}\:\:\frac{\mathrm{1}}{{a}+{b}\:\mathrm{cos}\:{x}}\:{dx},\:{a}>\mathrm{0}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\frac{\pi}{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\:, \\ $$$$\mathrm{then}\:\underset{\:\mathrm{0}} {\overset{\pi} {\int}}\:\:\:\frac{\mathrm{1}}{\left({a}+{b}\:\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\:{dx}\:= \\ $$

Question Number 64266 Answers: 1 Comments: 0

∫_(1/e) ^e ∣ log x ∣ dx =

$$\:\underset{\mathrm{1}/{e}} {\overset{{e}} {\int}}\:\mid\:\mathrm{log}\:{x}\:\mid\:{dx}\:= \\ $$

Pg 1472 Pg 1473 Pg 1474 Pg 1475 Pg 1476 Pg 1477 Pg 1478 Pg 1479 Pg 1480 Pg 1481

Contact: [email protected]