Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1469

Question Number 64302 Answers: 0 Comments: 0

Question Number 64300 Answers: 0 Comments: 0

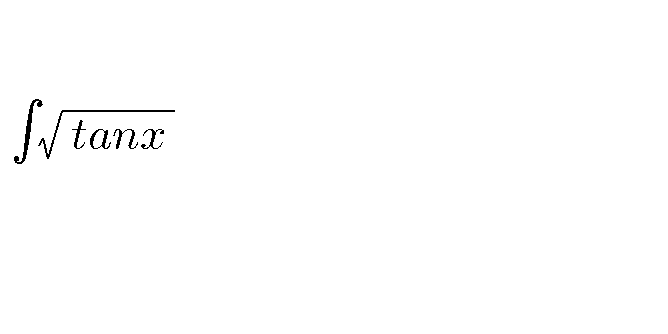
Question Number 64299 Answers: 0 Comments: 0

Question Number 64297 Answers: 0 Comments: 0

Question Number 64295 Answers: 0 Comments: 0

Question Number 64289 Answers: 2 Comments: 2

Question Number 64287 Answers: 0 Comments: 3

Question Number 64284 Answers: 0 Comments: 0

Find all the integer solution 3x^2 + 1 = 4y^3

$$\mathrm{Find}\:\mathrm{all}\:\mathrm{the}\:\mathrm{integer}\:\mathrm{solution}\:\:\:\:\:\:\:\mathrm{3x}^{\mathrm{2}} \:+\:\mathrm{1}\:\:=\:\:\mathrm{4y}^{\mathrm{3}} \\ $$

Question Number 64253 Answers: 0 Comments: 1

Question Number 64251 Answers: 0 Comments: 0

Question Number 64250 Answers: 0 Comments: 0

Question Number 64246 Answers: 3 Comments: 0

Question Number 64240 Answers: 1 Comments: 0

Question Number 64238 Answers: 0 Comments: 2

∫ln(x−5)/x^2 +110x−5dx

$$\int{ln}\left({x}−\mathrm{5}\right)/{x}^{\mathrm{2}} +\mathrm{110}{x}−\mathrm{5}{dx} \\ $$

Question Number 64227 Answers: 1 Comments: 0

∫(1/(x^6 +x^3 ))dx=?

$$\int\frac{\mathrm{1}}{{x}^{\mathrm{6}} +{x}^{\mathrm{3}} }{dx}=? \\ $$

Question Number 64225 Answers: 1 Comments: 0

Solution of the equation ∫_(√2) ^x (dx/(x (√(x^2 −1)))) = (π/(12)) is x = _____.

$$\mathrm{Solution}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\underset{\sqrt{\mathrm{2}}} {\overset{{x}} {\int}}\:\:\:\frac{{dx}}{{x}\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:=\:\frac{\pi}{\mathrm{12}}\:\:\mathrm{is}\:\:{x}\:=\:\_\_\_\_\_. \\ $$

Question Number 64224 Answers: 0 Comments: 1

∫x_x dx ∫x^x dx

$$\int{x}_{{x}} {dx} \\ $$$$ \\ $$$$\int{x}^{{x}} {dx} \\ $$

Question Number 64213 Answers: 0 Comments: 2

∫(1/(x!))dx=?

$$\int\frac{\mathrm{1}}{{x}!}{dx}=? \\ $$

Question Number 64267 Answers: 1 Comments: 1

If ∫_( 0) ^π (1/(a+b cos x)) dx, a>0 is equal to (π/(√(a^2 −b^2 ))) , then ∫_( 0) ^π (1/((a+b cos x)^2 )) dx =

$$\mathrm{If}\:\underset{\:\mathrm{0}} {\overset{\pi} {\int}}\:\:\frac{\mathrm{1}}{{a}+{b}\:\mathrm{cos}\:{x}}\:{dx},\:{a}>\mathrm{0}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\frac{\pi}{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\:, \\ $$$$\mathrm{then}\:\underset{\:\mathrm{0}} {\overset{\pi} {\int}}\:\:\:\frac{\mathrm{1}}{\left({a}+{b}\:\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\:{dx}\:= \\ $$

Question Number 64266 Answers: 1 Comments: 0

∫_(1/e) ^e ∣ log x ∣ dx =

$$\:\underset{\mathrm{1}/{e}} {\overset{{e}} {\int}}\:\mid\:\mathrm{log}\:{x}\:\mid\:{dx}\:= \\ $$

Question Number 64265 Answers: 1 Comments: 2

If ∫_(log 2) ^x (1/(√(e^x −1))) dx = (π/6), then x =

$$\mathrm{If}\:\underset{\mathrm{log}\:\mathrm{2}} {\overset{{x}} {\int}}\:\:\frac{\mathrm{1}}{\sqrt{{e}^{{x}} −\mathrm{1}}}\:{dx}\:=\:\frac{\pi}{\mathrm{6}},\:\mathrm{then}\:{x}\:= \\ $$

Question Number 64218 Answers: 0 Comments: 4

so goodbye everybody i am leaving this platform

$${so}\:{goodbye}\:{everybody}\:{i}\:{am}\:{leaving}\:{this}\:{platform} \\ $$

Question Number 64269 Answers: 1 Comments: 0

∫_(−π) ^π [cos px−sin qx]^2 dx, where p, q are integers is equal to

$$\underset{−\pi} {\overset{\pi} {\int}}\:\left[\mathrm{cos}\:{px}−\mathrm{sin}\:{qx}\right]^{\mathrm{2}} {dx},\:\mathrm{where}\:{p},\:{q}\:\mathrm{are}\: \\ $$$$\mathrm{integers}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$

Question Number 64268 Answers: 0 Comments: 1

lim_(n→∞) ((1^(99) +2^(99) +...+ n^(99) )/n^(100) ) =

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}^{\mathrm{99}} +\mathrm{2}^{\mathrm{99}} +...+\:{n}^{\mathrm{99}} }{{n}^{\mathrm{100}} }\:= \\ $$

Question Number 64270 Answers: 1 Comments: 0

∫((5sin(x) cos(x))/((cos(x)+1))^(1/3) ) dx

$$\int\frac{\mathrm{5}{sin}\left({x}\right)\:{cos}\left({x}\right)}{\sqrt[{\mathrm{3}}]{{cos}\left({x}\right)+\mathrm{1}}}\:{dx} \\ $$

Question Number 64204 Answers: 1 Comments: 1

Pg 1464 Pg 1465 Pg 1466 Pg 1467 Pg 1468 Pg 1469 Pg 1470 Pg 1471 Pg 1472 Pg 1473

Contact: info@tinkutara.com