
AllQuestion and Answers: Page 1467
Question Number 65380 Answers: 1 Comments: 1

Question Number 65387 Answers: 0 Comments: 0
Question Number 65386 Answers: 0 Comments: 1
Question Number 65372 Answers: 0 Comments: 4
$${I}=\int_{\mathrm{1}} ^{{e}} \:\frac{{dx}}{{x}\left(\mathrm{1}+{ln}^{\mathrm{2}} {x}\right)} \\ $$
Question Number 65367 Answers: 2 Comments: 1

Question Number 65366 Answers: 2 Comments: 2

Question Number 65365 Answers: 2 Comments: 0
Question Number 65359 Answers: 0 Comments: 0
Question Number 65356 Answers: 1 Comments: 1
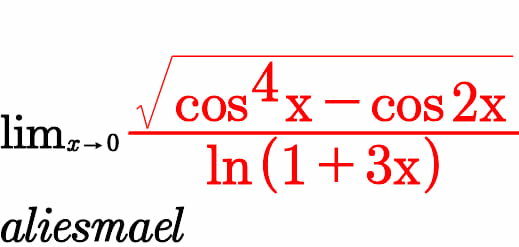
Question Number 65355 Answers: 2 Comments: 1
Question Number 65354 Answers: 0 Comments: 3
$${find}\:\:\int\:\:\:\:\:\:\frac{{dx}}{\sqrt{{x}^{\mathrm{2}} +{x}−\mathrm{2}}} \\ $$$$ \\ $$
Question Number 65352 Answers: 0 Comments: 1
Question Number 65347 Answers: 1 Comments: 0

Question Number 65345 Answers: 1 Comments: 4
Question Number 65335 Answers: 0 Comments: 0

Question Number 65334 Answers: 1 Comments: 0
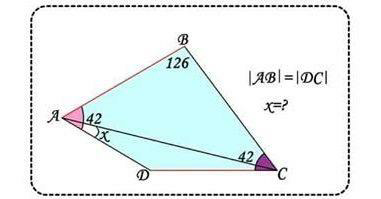
Question Number 65332 Answers: 0 Comments: 1

Question Number 65333 Answers: 1 Comments: 1
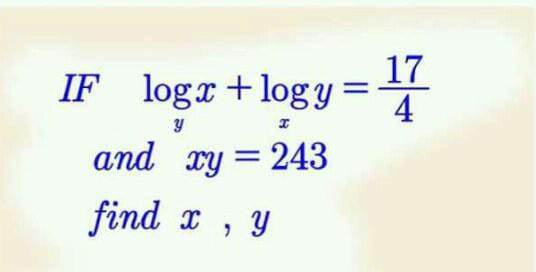
Question Number 65314 Answers: 0 Comments: 1

Question Number 65312 Answers: 0 Comments: 2

Question Number 65307 Answers: 1 Comments: 0
Question Number 65325 Answers: 1 Comments: 3
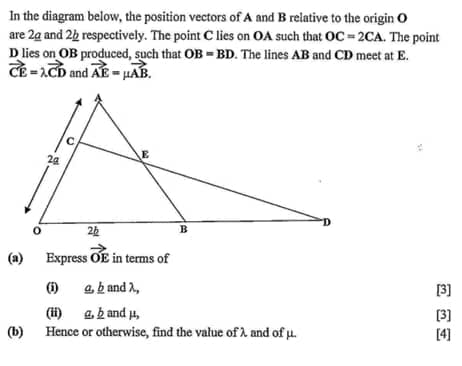
Question Number 65324 Answers: 0 Comments: 3

Question Number 65321 Answers: 0 Comments: 0

Question Number 65320 Answers: 0 Comments: 1

Question Number 65319 Answers: 3 Comments: 2
Pg 1462 Pg 1463 Pg 1464 Pg 1465 Pg 1466 Pg 1467 Pg 1468 Pg 1469 Pg 1470 Pg 1471
