Question and Answers Forum

AllQuestion and Answers: Page 1446

Question Number 67517 Answers: 0 Comments: 0

let z ∈C and ∣z∣<1 prove that (z/(1−z^2 )) +(z^2 /(1−z^4 )) +.....+(z^2^n /(1−z^2^(n+1) ))+...=(z/(1−z)) (z/(1+z)) +((2z^2 )/(1+z^2 )) +....+((2^n z^2^n )/(1+z^2^n )) +....=(z/(1−z))

$${let}\:{z}\:\in{C}\:{and}\:\mid{z}\mid<\mathrm{1}\:\:{prove}\:{that} \\ $$$$\frac{{z}}{\mathrm{1}−{z}^{\mathrm{2}} }\:+\frac{{z}^{\mathrm{2}} }{\mathrm{1}−{z}^{\mathrm{4}} }\:+.....+\frac{{z}^{\mathrm{2}^{{n}} } }{\mathrm{1}−{z}^{\mathrm{2}^{{n}+\mathrm{1}} } }+...=\frac{{z}}{\mathrm{1}−{z}} \\ $$$$\frac{{z}}{\mathrm{1}+{z}}\:+\frac{\mathrm{2}{z}^{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{2}} }\:+....+\frac{\mathrm{2}^{{n}} \:{z}^{\mathrm{2}^{{n}} } }{\mathrm{1}+\mathrm{z}^{\mathrm{2}^{\mathrm{n}} } }\:+....=\frac{\mathrm{z}}{\mathrm{1}−\mathrm{z}} \\ $$

Question Number 67516 Answers: 2 Comments: 2

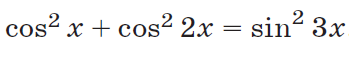
Question Number 67514 Answers: 1 Comments: 1

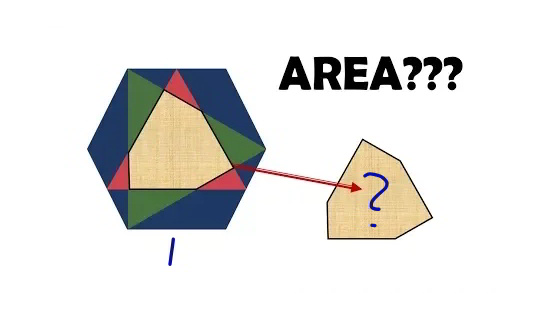
Question Number 67513 Answers: 0 Comments: 0

∫x^(n ) lnx/n^x dx

$$\int{x}^{{n}\:} {lnx}/{n}^{{x}} \:{dx} \\ $$

Question Number 67501 Answers: 2 Comments: 2

Show that 1n^3 + 2n + 3n^2 is divisible by 2 and 3 for all positive integers n.

$$\mathrm{Show}\:\mathrm{that}\:\:\mathrm{1n}^{\mathrm{3}} \:+\:\mathrm{2n}\:+\:\mathrm{3n}^{\mathrm{2}} \:\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{2}\:\mathrm{and}\:\mathrm{3}\:\mathrm{for}\:\mathrm{all}\:\mathrm{positive}\:\mathrm{integers}\:\mathrm{n}. \\ $$

Question Number 67495 Answers: 0 Comments: 2

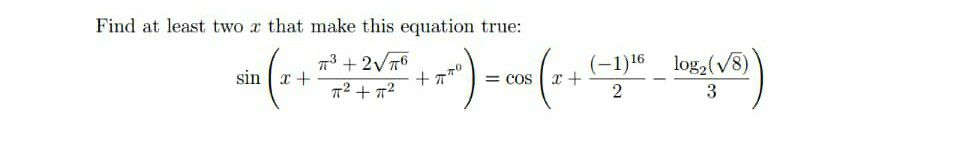
Question Number 67492 Answers: 0 Comments: 1

please check my comment to qu. 67471 I′ve been confusing myself...

$$\mathrm{please}\:\mathrm{check}\:\mathrm{my}\:\mathrm{comment}\:\mathrm{to}\:\mathrm{qu}.\:\mathrm{67471} \\ $$$$\mathrm{I}'\mathrm{ve}\:\mathrm{been}\:\mathrm{confusing}\:\mathrm{myself}... \\ $$

Question Number 67482 Answers: 0 Comments: 1

I have tried to solve Q#67299 Please see and give critical remarks

$${I}\:{have}\:{tried}\:{to}\:{solve}\:{Q}#\mathrm{67299} \\ $$$${Please}\:{see}\:{and}\:{give}\:{critical}\:{remarks} \\ $$

Question Number 67471 Answers: 0 Comments: 4

Evaluate:∫(√(x(√(x+1)))) dx

$$\boldsymbol{{Evaluate}}:\int\sqrt{{x}\sqrt{{x}+\mathrm{1}}}\:{dx} \\ $$

Question Number 67467 Answers: 0 Comments: 0

Find f(x)=∫_0 ^∞ (( tlnt)/((1+t^2 )^x )) dt

$$ \\ $$$$ \\ $$$${Find}\:\:\:\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\:{tlnt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{x}} }\:{dt}\: \\ $$

Question Number 67466 Answers: 0 Comments: 0

let consider for all n≥1 the real (t)_n =t(t+1).....(t+n−1) Find L_n = ∫_0 ^∞ (((t)_1 )/((t)_(n+1) )) dt

$$ \\ $$$$ \\ $$$${let}\:{consider}\:\:\:{for}\:{all}\:{n}\geqslant\mathrm{1}\:{the}\:{real}\:\left({t}\right)_{{n}} \:={t}\left({t}+\mathrm{1}\right).....\left({t}+{n}−\mathrm{1}\right) \\ $$$${Find}\:\:\:{L}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left({t}\right)_{\mathrm{1}} }{\left({t}\right)_{{n}+\mathrm{1}} }\:{dt} \\ $$

Question Number 67465 Answers: 0 Comments: 4

let consider a function g defined by g(a)=∫_0 ^1 (dx/(√((1−x)(1+ax)))) Give the defined Domain of g and simplify g.

$$ \\ $$$$ \\ $$$$\:\:{let}\:{consider}\:{a}\:{function}\:{g}\:{defined}\:{by}\:\:\:{g}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{\sqrt{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{ax}\right)}}\:\: \\ $$$${Give}\:{the}\:{defined}\:{Domain}\:{of}\:{g}\:\:{and}\:{simplify}\:{g}. \\ $$

Question Number 67464 Answers: 1 Comments: 0

prove Cos(((2π)/7))+Cos(((4π)/7))+Cos(((8π)/7))=−(1/2)

$$\mathrm{prove}\:\:\:\mathrm{Cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)+\mathrm{Cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)+\mathrm{Cos}\left(\frac{\mathrm{8}\pi}{\mathrm{7}}\right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Question Number 67463 Answers: 1 Comments: 3

Find Find K=∫_0 ^(π/2) (√(tanθ)) dθ

$${Find} \\ $$$${Find}\:\:\:{K}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{tan}\theta}\:{d}\theta\: \\ $$

Question Number 67462 Answers: 0 Comments: 2

Calculate when a,b are positive reals f(a,b)= ∫_0 ^1 ((t^a −t^b )/(lnt)) dt

$$ \\ $$$$\:{Calculate}\:{when}\:{a},{b}\:{are}\:{positive}\:{reals}\:\:\:{f}\left({a},{b}\right)=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}^{{a}} −{t}^{{b}} }{{lnt}}\:{dt}\: \\ $$

Question Number 67461 Answers: 0 Comments: 0

find the value of Σ_(p=0) ^∞ (((−1)^p )/((2p+1)^2 ))

$${find}\:{the}\:{value}\:{of}\:\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{p}} }{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Question Number 67454 Answers: 0 Comments: 2

Question Number 67481 Answers: 0 Comments: 2

p is a prime number such that (1+p)^p ≡2[7] find all k such that p≡k[42]

$${p}\:{is}\:{a}\:{prime}\:{number}\:{such}\:{that}\:\left(\mathrm{1}+{p}\right)^{{p}} \equiv\mathrm{2}\left[\mathrm{7}\right] \\ $$$${find}\:{all}\:{k}\:{such}\:{that}\:{p}\equiv{k}\left[\mathrm{42}\right] \\ $$

Question Number 67431 Answers: 1 Comments: 1

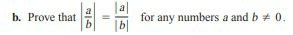
Question Number 67430 Answers: 2 Comments: 2

Question Number 67422 Answers: 1 Comments: 2

Question Number 68043 Answers: 1 Comments: 1

∫_(π/2) ^π e^(cosx) (√(1−e^(cosx) )) sinx dx

$$\int_{\pi/\mathrm{2}} ^{\pi} {e}^{{cosx}} \sqrt{\mathrm{1}−{e}^{{cosx}} }\:{sinx}\:{dx} \\ $$

Question Number 68728 Answers: 0 Comments: 0

dear scientist. i did some research on the energy obtained from the sun any other source by a liquid, of density ρ , velocity v, viscosity η and distance travelled d. i came out with the equation E = k ( vρ η^3 d^2 ) where k is a costant i still need to determine from more experiment. But please i want you guys great people to check if the equation is in confirmity and if atall it is correct so i can do some changes. thanks in advanced dear scientist.

$${dear}\:{scientist}. \\ $$$${i}\:{did}\:{some}\:{research}\:{on}\:{the}\:{energy}\:{obtained}\:{from}\:{the}\:{sun} \\ $$$${any}\:{other}\:{source}\:\:{by}\:{a}\:{liquid},\:{of}\:{density}\:\rho\:,\:{velocity}\:\:{v},\:\:{viscosity}\:\eta\:{and}\:{distance}\: \\ $$$${travelled}\:\:\:{d}. \\ $$$$ \\ $$$${i}\:{came}\:{out}\:{with}\:{the}\:{equation}\: \\ $$$$\:\:\:{E}\:=\:{k}\:\left(\:{v}\rho\:\eta^{\mathrm{3}} \:{d}^{\mathrm{2}} \right) \\ $$$${where}\:\:{k}\:{is}\:{a}\:{costant}\:{i}\:{still}\:{need}\:{to}\:{determine}\:{from}\:{more} \\ $$$${experiment}.\:{But}\:{please}\:{i}\:{want}\:{you}\:{guys}\:\:{great}\:{people}\:{to}\: \\ $$$${check}\:{if}\:{the}\:{equation}\:{is}\:{in}\:{confirmity}\:{and}\:{if}\:{atall}\:{it}\:{is}\:{correct} \\ $$$${so}\:{i}\:{can}\:{do}\:{some}\:{changes}. \\ $$$$ \\ $$$${thanks}\:{in}\:{advanced}\:\:{dear}\:{scientist}. \\ $$$$ \\ $$

Question Number 67413 Answers: 0 Comments: 0

Question Number 67398 Answers: 0 Comments: 2

solve the defrintion eguation (xp^2 −p+2x)=0 when p=dy/dx

$${solve}\:{the}\:{defrintion}\:{eguation}\:\left({xp}^{\mathrm{2}} −{p}+\mathrm{2}{x}\right)=\mathrm{0} \\ $$$${when}\:{p}={dy}/{dx} \\ $$

Question Number 67396 Answers: 0 Comments: 2

Pg 1441 Pg 1442 Pg 1443 Pg 1444 Pg 1445 Pg 1446 Pg 1447 Pg 1448 Pg 1449 Pg 1450

Contact: [email protected]