
AllQuestion and Answers: Page 1436
Question Number 68595 Answers: 0 Comments: 1
Question Number 68594 Answers: 0 Comments: 0
Question Number 68593 Answers: 0 Comments: 1
Question Number 68592 Answers: 0 Comments: 2
Question Number 68591 Answers: 0 Comments: 6

Question Number 68589 Answers: 1 Comments: 0
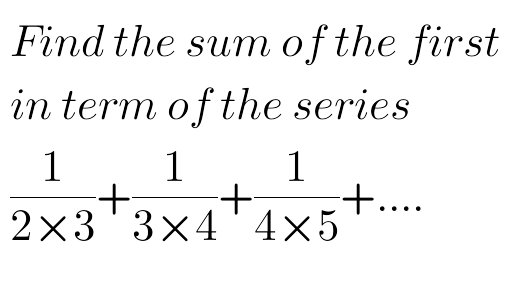
Question Number 68632 Answers: 0 Comments: 0
Question Number 68554 Answers: 0 Comments: 4

Question Number 68549 Answers: 1 Comments: 3
$${y}=\frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${y}^{−\mathrm{1}} =... \\ $$
Question Number 68546 Answers: 1 Comments: 0
Question Number 68541 Answers: 1 Comments: 1

Question Number 68537 Answers: 2 Comments: 0

Question Number 68532 Answers: 0 Comments: 0

Question Number 68521 Answers: 0 Comments: 1
Question Number 68517 Answers: 0 Comments: 0

Question Number 68515 Answers: 1 Comments: 2

Question Number 68510 Answers: 1 Comments: 0
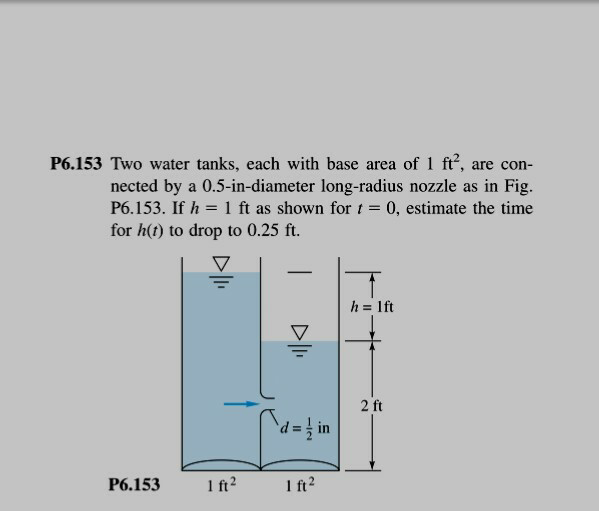
Question Number 68509 Answers: 0 Comments: 0

Question Number 68508 Answers: 0 Comments: 0

Question Number 68506 Answers: 0 Comments: 0
Question Number 68503 Answers: 0 Comments: 8

Question Number 68524 Answers: 1 Comments: 0

Question Number 68528 Answers: 0 Comments: 0
Question Number 68495 Answers: 1 Comments: 1
Question Number 68493 Answers: 1 Comments: 0
Question Number 68482 Answers: 0 Comments: 1
Pg 1431 Pg 1432 Pg 1433 Pg 1434 Pg 1435 Pg 1436 Pg 1437 Pg 1438 Pg 1439 Pg 1440
