Question and Answers Forum

AllQuestion and Answers: Page 1434

Question Number 66680 Answers: 0 Comments: 2

calculate Σ_(n=1) ^∞ (2^n /(3^n (2n^3 +n^2 −5n +2)))

$${calculate}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\frac{\mathrm{2}^{{n}} }{\mathrm{3}^{{n}} \left(\mathrm{2}{n}^{\mathrm{3}} \:+{n}^{\mathrm{2}} −\mathrm{5}{n}\:+\mathrm{2}\right)} \\ $$

Question Number 66670 Answers: 1 Comments: 1

Question Number 66667 Answers: 1 Comments: 3

Question Number 66664 Answers: 0 Comments: 0

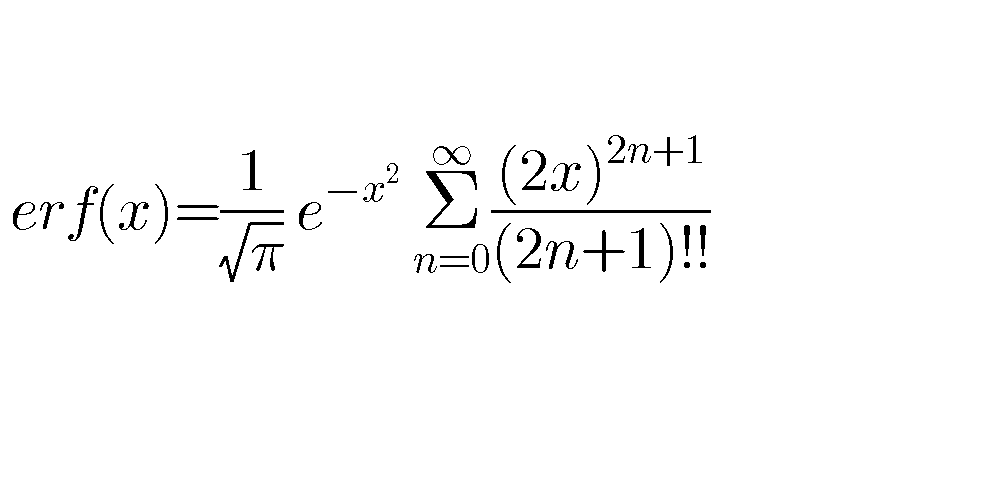
Question Number 66656 Answers: 1 Comments: 1

Question Number 66640 Answers: 0 Comments: 6

lim_(x→4) ((((2+x(√x)))^(1/3) −2)/(8−x(√x)))=?

$$\: \\ $$$$\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{4}} {\boldsymbol{{lim}}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}+\boldsymbol{{x}}\sqrt{\boldsymbol{{x}}}}−\mathrm{2}}{\mathrm{8}−\boldsymbol{{x}}\sqrt{\boldsymbol{{x}}}}=? \\ $$$$\: \\ $$

Question Number 66629 Answers: 0 Comments: 1

Question Number 66627 Answers: 1 Comments: 4

Question Number 66621 Answers: 0 Comments: 7

Question Number 66620 Answers: 0 Comments: 3

find lim_(n→∞) I_n I_n =∫_0 ^∞ (dx/((1+coth (nx))^n )) ,n≥1

$${find}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{I}_{{n}} \\ $$$${I}_{{n}} =\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+\mathrm{coth}\:\left({nx}\right)\right)^{{n}} }\:,{n}\geqslant\mathrm{1} \\ $$$$ \\ $$

Question Number 66619 Answers: 1 Comments: 0

solve for x,y∈R ((√(1+x^2 ))/(ln (x+(√(1+x^2 )))))=((√(1+y^2 ))/(ln (y+(√(1+y^2 )))))

$${solve}\:{for}\:{x},{y}\in{R} \\ $$$$\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)}=\frac{\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }}{\mathrm{ln}\:\left({y}+\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }\right)} \\ $$

Question Number 66602 Answers: 2 Comments: 3

Question Number 66601 Answers: 1 Comments: 1

Question Number 66599 Answers: 0 Comments: 2

Question Number 66589 Answers: 2 Comments: 5

∫((sinx)/(1+sinx+sin2x))dx

$$\int\frac{{sinx}}{\mathrm{1}+{sinx}+{sin}\mathrm{2}{x}}{dx} \\ $$

Question Number 66564 Answers: 0 Comments: 0

Question Number 66561 Answers: 1 Comments: 2

evaluate ∫_0 ^2 ∣ x+ 2∣ dx.

$${evaluate}\: \\ $$$$\:\:\int_{\mathrm{0}} ^{\mathrm{2}} \mid\:{x}+\:\mathrm{2}\mid\:{dx}. \\ $$

Question Number 66562 Answers: 1 Comments: 1

given that ∣z − i∣ = ∣z − 4 +3 i∣ sketch the locus of z find the catersian equation of this locus.

$${given}\:{that}\:\:\mid{z}\:−\:\mathrm{i}\mid\:=\:\mid{z}\:−\:\mathrm{4}\:+\mathrm{3}\:\mathrm{i}\mid \\ $$$${sketch}\:{the}\:{locus}\:{of}\:\:{z} \\ $$$${find}\:{the}\:{catersian}\:{equation}\:{of}\:{this}\:{locus}. \\ $$

Question Number 66550 Answers: 0 Comments: 2

∫_0 ^1 ∫_((y/2) ) ^((1/2) ) e^(−x^2 ) dxdy=?

$$\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\frac{{y}}{\mathrm{2}}\:} ^{\frac{\mathrm{1}}{\mathrm{2}}\:} {e}^{−{x}^{\mathrm{2}} } {dxdy}=? \\ $$

Question Number 66549 Answers: 0 Comments: 0

((n^2 !)/((n!)^n ))=natural number.

$$\frac{\mathrm{n}^{\mathrm{2}} !}{\left(\mathrm{n}!\right)^{\mathrm{n}} }=\mathrm{natural}\:\mathrm{number}. \\ $$

Question Number 66548 Answers: 0 Comments: 1

Evaluate:∫(√(x(√(x+1)) ))dx

$$\boldsymbol{{Evaluate}}:\int\sqrt{{x}\sqrt{{x}+\mathrm{1}}\:}{dx} \\ $$

Question Number 66546 Answers: 0 Comments: 6

Question Number 66544 Answers: 1 Comments: 0

Find a, b, c which fulfill lim_(x→0) ((x(a + b cos x) − c sin x)/x^5 ) = 1

$${Find}\:\:{a},\:{b},\:{c}\:\:{which}\:\:{fulfill}\:\:\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{{x}\left({a}\:+\:{b}\:\mathrm{cos}\:{x}\right)\:−\:{c}\:\mathrm{sin}\:{x}}{{x}^{\mathrm{5}} }\:\:=\:\:\mathrm{1} \\ $$

Question Number 66543 Answers: 2 Comments: 1

3^x =3x x=?

$$\:\mathrm{3}^{\boldsymbol{{x}}} =\mathrm{3}\boldsymbol{{x}} \\ $$$$\: \\ $$$$\:\boldsymbol{{x}}=? \\ $$

Question Number 66540 Answers: 0 Comments: 0

graph the function r^2 =cos(2θ) and find the area?

$${graph}\:{the}\:{function}\:{r}^{\mathrm{2}} ={cos}\left(\mathrm{2}\theta\right)\:{and}\:{find}\:{the}\:{area}? \\ $$

Question Number 66536 Answers: 0 Comments: 0

∫ln^(10) (x) sin^7 (x) dx

$$\int{ln}^{\mathrm{10}} \left({x}\right)\:{sin}^{\mathrm{7}} \left({x}\right)\:{dx} \\ $$

Pg 1429 Pg 1430 Pg 1431 Pg 1432 Pg 1433 Pg 1434 Pg 1435 Pg 1436 Pg 1437 Pg 1438

Contact: info@tinkutara.com