
AllQuestion and Answers: Page 1428
Question Number 69074 Answers: 0 Comments: 0
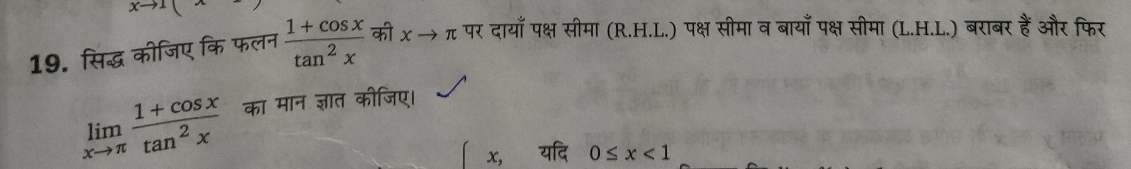
Question Number 69073 Answers: 0 Comments: 3
Question Number 69072 Answers: 0 Comments: 0

Question Number 69064 Answers: 1 Comments: 3

Question Number 69106 Answers: 0 Comments: 0

Question Number 69105 Answers: 0 Comments: 0

Question Number 69104 Answers: 0 Comments: 3

Question Number 69111 Answers: 1 Comments: 2

Question Number 69110 Answers: 0 Comments: 3
Question Number 69098 Answers: 1 Comments: 3
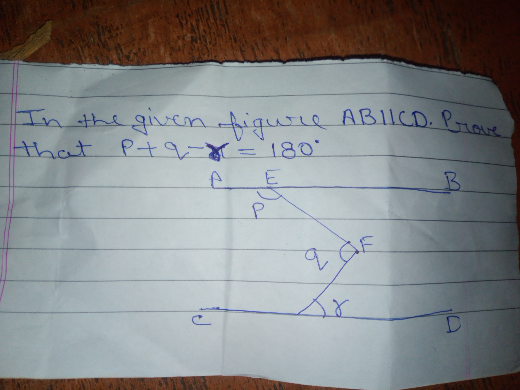
Question Number 69046 Answers: 0 Comments: 4

Question Number 69045 Answers: 2 Comments: 0
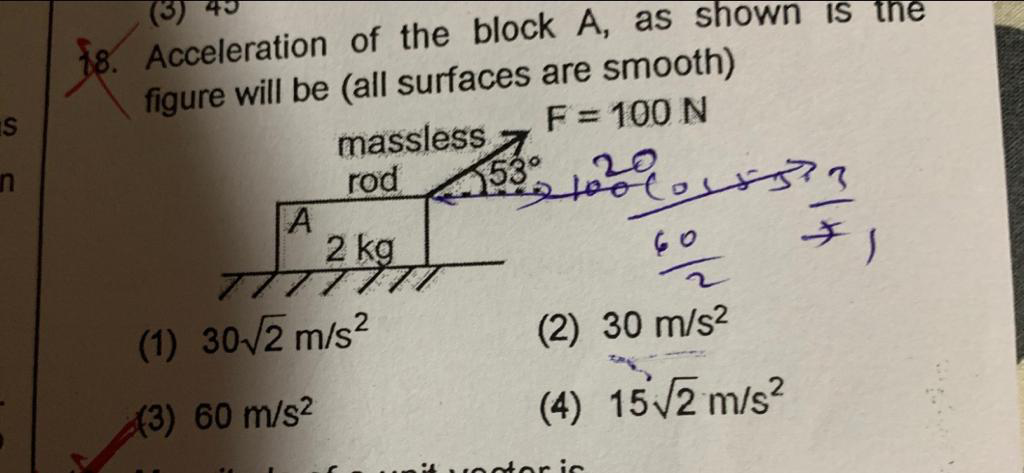
Question Number 69034 Answers: 2 Comments: 0

Question Number 69044 Answers: 1 Comments: 0
Question Number 69027 Answers: 1 Comments: 2

Question Number 69020 Answers: 0 Comments: 1
Question Number 69014 Answers: 1 Comments: 0
Question Number 69010 Answers: 0 Comments: 8
Question Number 68991 Answers: 1 Comments: 0
Question Number 69174 Answers: 0 Comments: 3
Question Number 69173 Answers: 0 Comments: 0
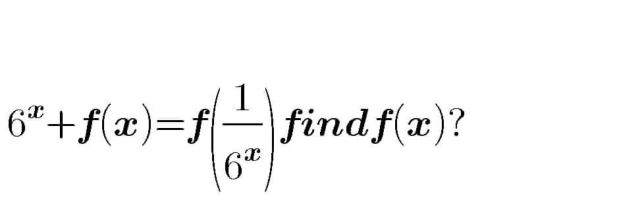
Question Number 68977 Answers: 1 Comments: 4

Question Number 68970 Answers: 1 Comments: 0
$$\int\frac{\mathrm{3}{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{15}} }\:{dt} \\ $$
Question Number 68967 Answers: 1 Comments: 0

Question Number 68966 Answers: 0 Comments: 4
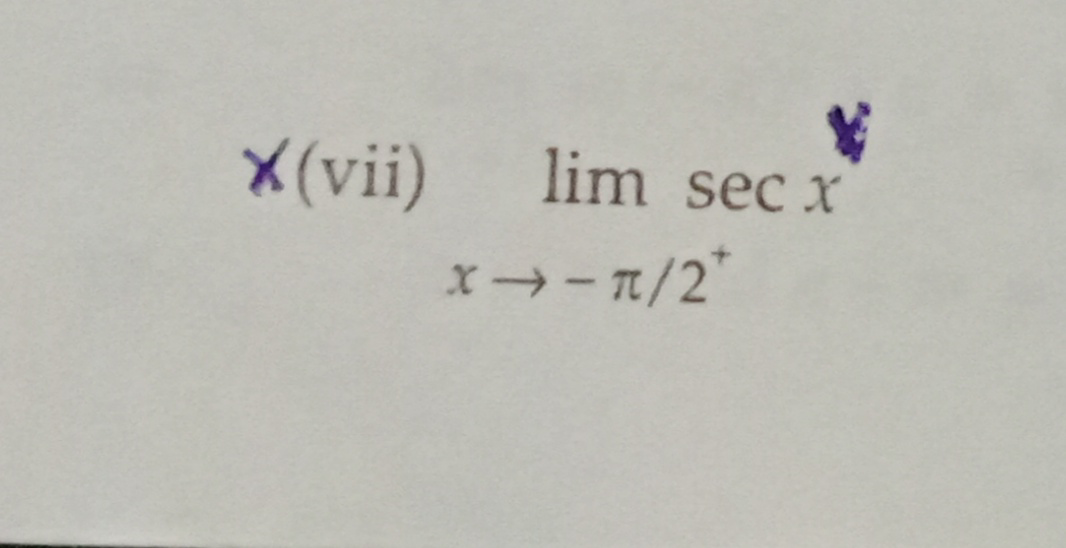
Question Number 68965 Answers: 0 Comments: 2

Pg 1423 Pg 1424 Pg 1425 Pg 1426 Pg 1427 Pg 1428 Pg 1429 Pg 1430 Pg 1431 Pg 1432
