
AllQuestion and Answers: Page 1427
Question Number 69645 Answers: 1 Comments: 0
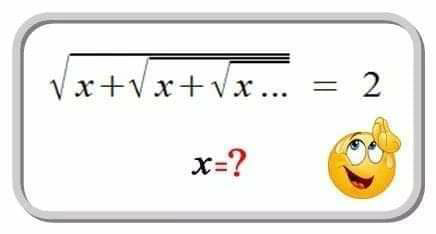
Question Number 69644 Answers: 2 Comments: 0

Question Number 69643 Answers: 1 Comments: 0
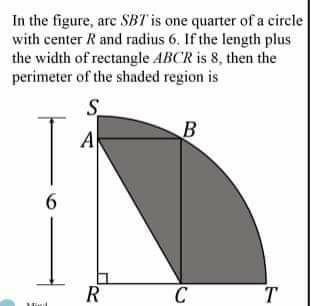
Question Number 69641 Answers: 0 Comments: 0
Question Number 69637 Answers: 1 Comments: 0
Question Number 69623 Answers: 1 Comments: 0
$$\int\frac{\mathrm{1}}{\sqrt{{x}}\:+\:\sqrt[{\mathrm{3}}]{{x}}}\:{dx} \\ $$
Question Number 69616 Answers: 0 Comments: 4
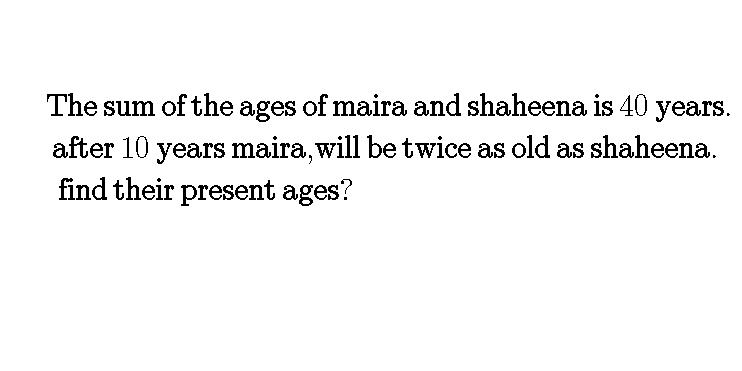
Question Number 69606 Answers: 0 Comments: 0

Question Number 69603 Answers: 1 Comments: 0
Question Number 69597 Answers: 1 Comments: 1

Question Number 69594 Answers: 1 Comments: 0

Question Number 69593 Answers: 1 Comments: 2

Question Number 69576 Answers: 1 Comments: 1
Question Number 69574 Answers: 1 Comments: 0

Question Number 69573 Answers: 0 Comments: 1

Question Number 69572 Answers: 1 Comments: 0

Question Number 69571 Answers: 1 Comments: 0

Question Number 69570 Answers: 0 Comments: 0

Question Number 69569 Answers: 2 Comments: 0
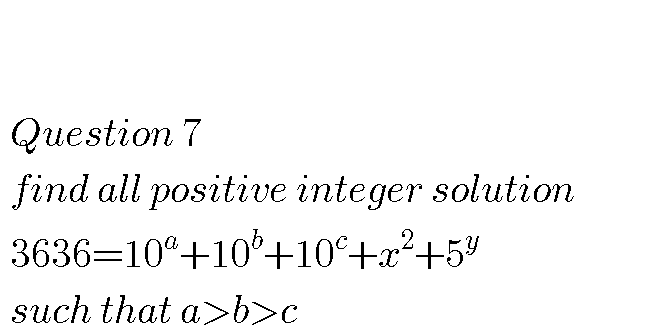
Question Number 69568 Answers: 1 Comments: 3

Question Number 69567 Answers: 0 Comments: 2

Question Number 69566 Answers: 1 Comments: 0

Question Number 69565 Answers: 0 Comments: 0

Question Number 69564 Answers: 0 Comments: 3
Question Number 69563 Answers: 0 Comments: 1
Question Number 69610 Answers: 0 Comments: 0

Pg 1422 Pg 1423 Pg 1424 Pg 1425 Pg 1426 Pg 1427 Pg 1428 Pg 1429 Pg 1430 Pg 1431
