
AllQuestion and Answers: Page 1424
Question Number 69567 Answers: 0 Comments: 2

Question Number 69566 Answers: 1 Comments: 0

Question Number 69565 Answers: 0 Comments: 0

Question Number 69564 Answers: 0 Comments: 3
Question Number 69563 Answers: 0 Comments: 1
Question Number 69610 Answers: 0 Comments: 0

Question Number 69609 Answers: 0 Comments: 2

Question Number 69608 Answers: 1 Comments: 2

Question Number 69607 Answers: 0 Comments: 4
Question Number 69557 Answers: 1 Comments: 0

Question Number 69620 Answers: 0 Comments: 1

Question Number 69545 Answers: 0 Comments: 2

Question Number 69538 Answers: 0 Comments: 0
Question Number 69535 Answers: 3 Comments: 1

Question Number 69586 Answers: 0 Comments: 0
Question Number 69502 Answers: 3 Comments: 2
$$\int\frac{\mathrm{3sinx}+\mathrm{4cosx}}{\mathrm{4sinx}+\mathrm{3cosx}}\mathrm{dx} \\ $$
Question Number 69500 Answers: 2 Comments: 0
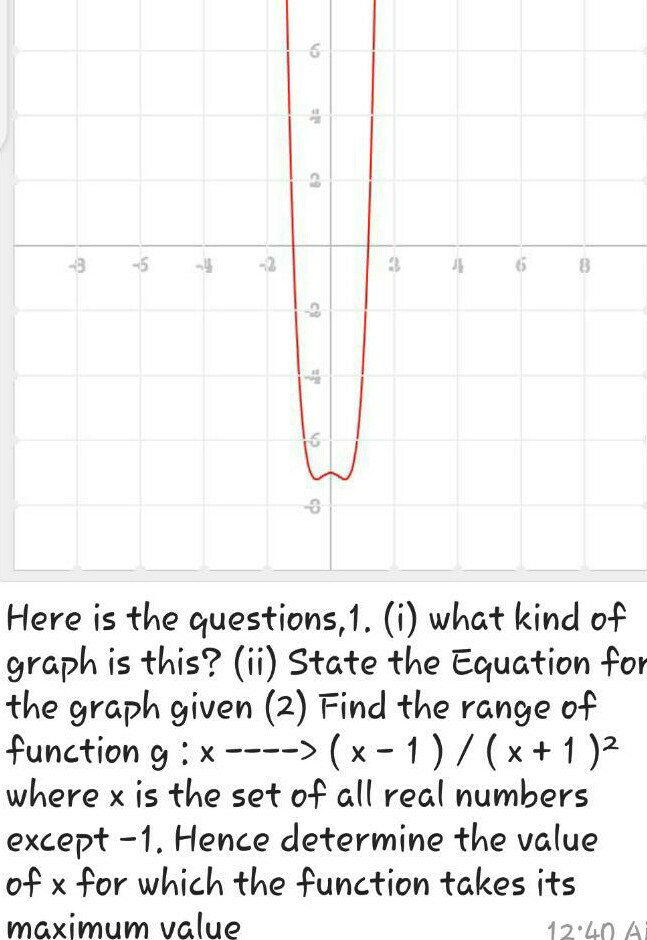
Question Number 69496 Answers: 0 Comments: 5
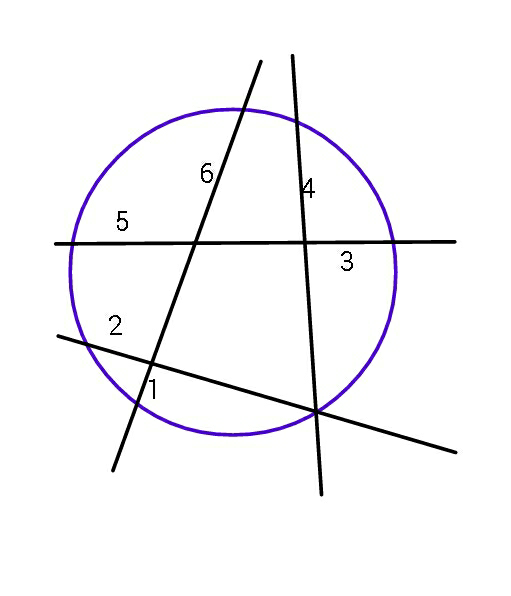
Question Number 69494 Answers: 1 Comments: 3

Question Number 69493 Answers: 0 Comments: 0

Question Number 69589 Answers: 0 Comments: 0
Question Number 69479 Answers: 0 Comments: 2
Question Number 69478 Answers: 0 Comments: 1
Question Number 69462 Answers: 0 Comments: 1
Question Number 69460 Answers: 0 Comments: 1
Question Number 69459 Answers: 0 Comments: 0

Pg 1419 Pg 1420 Pg 1421 Pg 1422 Pg 1423 Pg 1424 Pg 1425 Pg 1426 Pg 1427 Pg 1428
