
AllQuestion and Answers: Page 1423
Question Number 69681 Answers: 2 Comments: 2

Question Number 69680 Answers: 2 Comments: 0
Question Number 71918 Answers: 2 Comments: 2
Question Number 69667 Answers: 1 Comments: 0
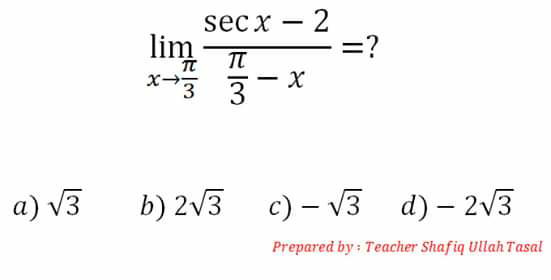
Question Number 69665 Answers: 1 Comments: 1

Question Number 69662 Answers: 1 Comments: 0
Question Number 69645 Answers: 1 Comments: 0
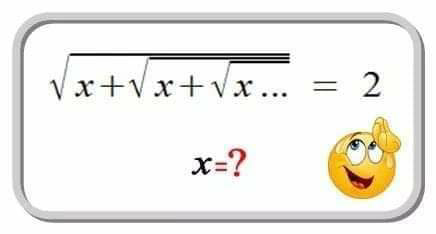
Question Number 69644 Answers: 2 Comments: 0

Question Number 69643 Answers: 1 Comments: 0
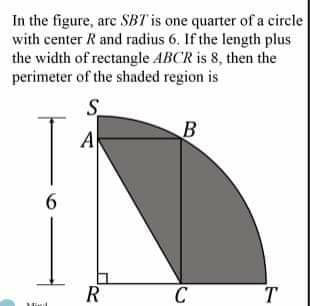
Question Number 69641 Answers: 0 Comments: 0
Question Number 69637 Answers: 1 Comments: 0
Question Number 69623 Answers: 1 Comments: 0
$$\int\frac{\mathrm{1}}{\sqrt{{x}}\:+\:\sqrt[{\mathrm{3}}]{{x}}}\:{dx} \\ $$
Question Number 69616 Answers: 0 Comments: 4
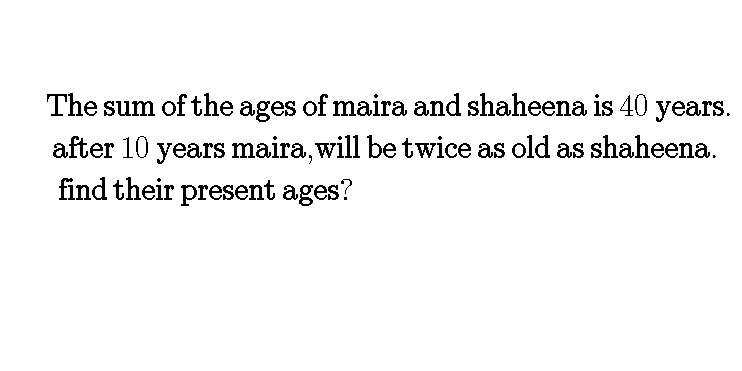
Question Number 69606 Answers: 0 Comments: 0

Question Number 69603 Answers: 1 Comments: 0
Question Number 69597 Answers: 1 Comments: 1

Question Number 69594 Answers: 1 Comments: 0

Question Number 69593 Answers: 1 Comments: 2

Question Number 69576 Answers: 1 Comments: 1
Question Number 69574 Answers: 1 Comments: 0

Question Number 69573 Answers: 0 Comments: 1

Question Number 69572 Answers: 1 Comments: 0

Question Number 69571 Answers: 1 Comments: 0

Question Number 69570 Answers: 0 Comments: 0

Question Number 69569 Answers: 2 Comments: 0
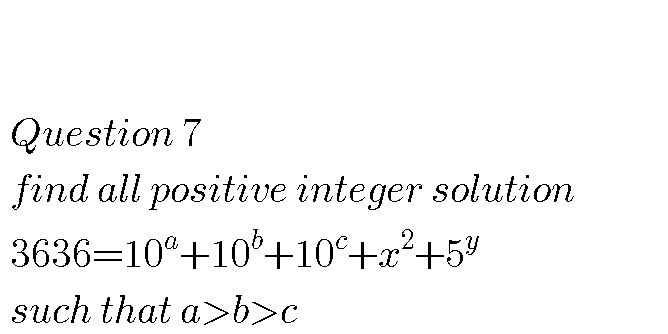
Question Number 69568 Answers: 1 Comments: 3

Pg 1418 Pg 1419 Pg 1420 Pg 1421 Pg 1422 Pg 1423 Pg 1424 Pg 1425 Pg 1426 Pg 1427
