
AllQuestion and Answers: Page 1421
Question Number 70592 Answers: 1 Comments: 1

Question Number 70590 Answers: 1 Comments: 1
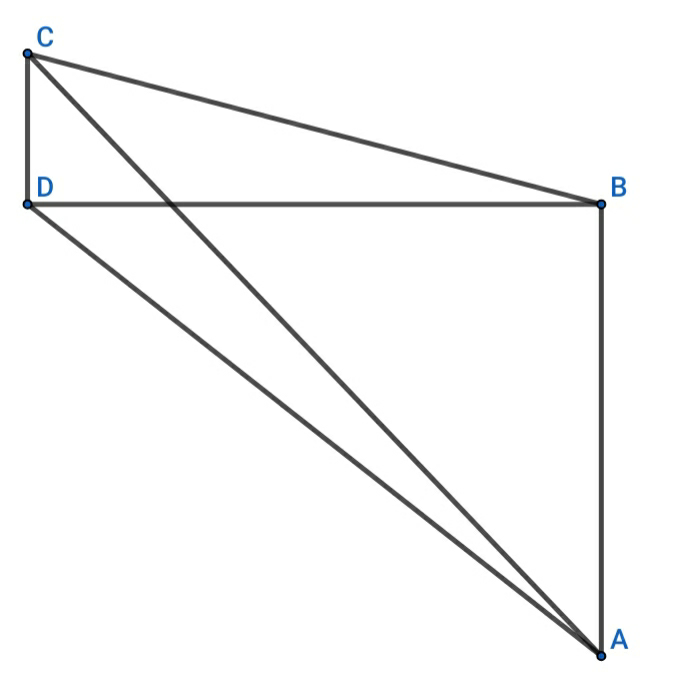
Question Number 70583 Answers: 1 Comments: 0
Question Number 70587 Answers: 0 Comments: 1

Question Number 70568 Answers: 0 Comments: 1

Question Number 70562 Answers: 0 Comments: 0
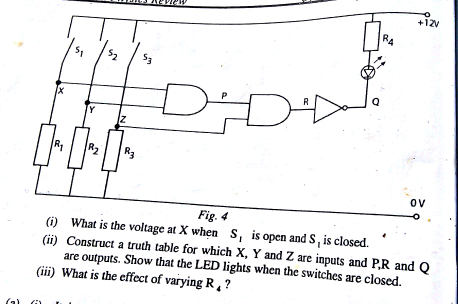
Question Number 70571 Answers: 0 Comments: 1

Question Number 70582 Answers: 0 Comments: 1
Question Number 70543 Answers: 0 Comments: 6

Question Number 70525 Answers: 1 Comments: 0
Question Number 70519 Answers: 0 Comments: 3

Question Number 70518 Answers: 2 Comments: 2
Question Number 70516 Answers: 1 Comments: 1

Question Number 70513 Answers: 0 Comments: 1
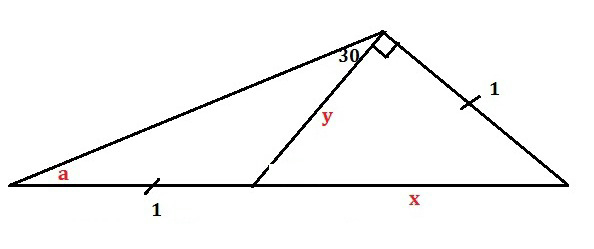
Question Number 70512 Answers: 1 Comments: 1
Question Number 70499 Answers: 0 Comments: 2

Question Number 70497 Answers: 1 Comments: 1
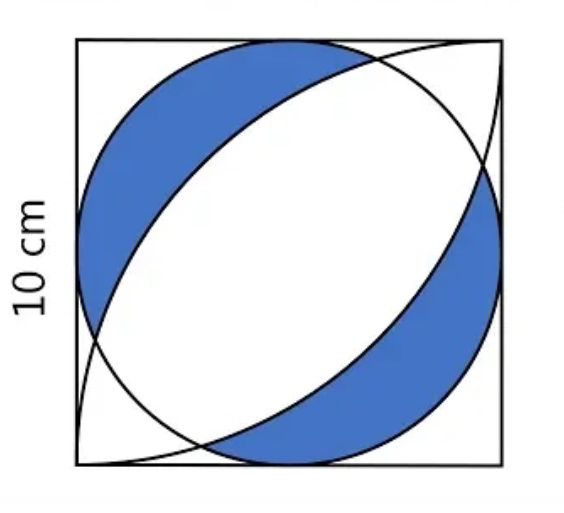
Question Number 70520 Answers: 0 Comments: 0

Question Number 70483 Answers: 1 Comments: 3
$$\int\frac{{ln}\mathrm{2}{x}}{{ln}\mathrm{4}{x}}.\frac{{dx}}{{x}} \\ $$
Question Number 70482 Answers: 1 Comments: 2
$$\int\frac{{sin}^{\mathrm{3}} {x}}{\sqrt{{cosx}}}{dx} \\ $$
Question Number 70473 Answers: 0 Comments: 1
Question Number 70503 Answers: 0 Comments: 3

Question Number 70460 Answers: 0 Comments: 2

Question Number 70452 Answers: 2 Comments: 4

Question Number 70448 Answers: 0 Comments: 0
Question Number 70446 Answers: 0 Comments: 4
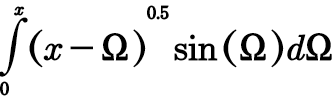
Pg 1416 Pg 1417 Pg 1418 Pg 1419 Pg 1420 Pg 1421 Pg 1422 Pg 1423 Pg 1424 Pg 1425
