
AllQuestion and Answers: Page 1420
Question Number 70710 Answers: 1 Comments: 0
Question Number 70713 Answers: 0 Comments: 1
Question Number 70705 Answers: 1 Comments: 0
$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{log}_{\mathrm{10}} \mathrm{x}\right)=? \\ $$
Question Number 70704 Answers: 1 Comments: 2
$$\mathrm{z}^{\mathrm{4}} −\mathrm{2z}^{\mathrm{2}} +\mathrm{2}=\mathrm{0} \\ $$
Question Number 70696 Answers: 1 Comments: 4
Question Number 70694 Answers: 1 Comments: 0
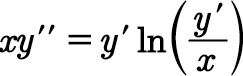
Question Number 70688 Answers: 0 Comments: 0

Question Number 70686 Answers: 2 Comments: 0
$${find}\:\int\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{6}} } \\ $$
Question Number 70679 Answers: 0 Comments: 2
Question Number 70672 Answers: 1 Comments: 1
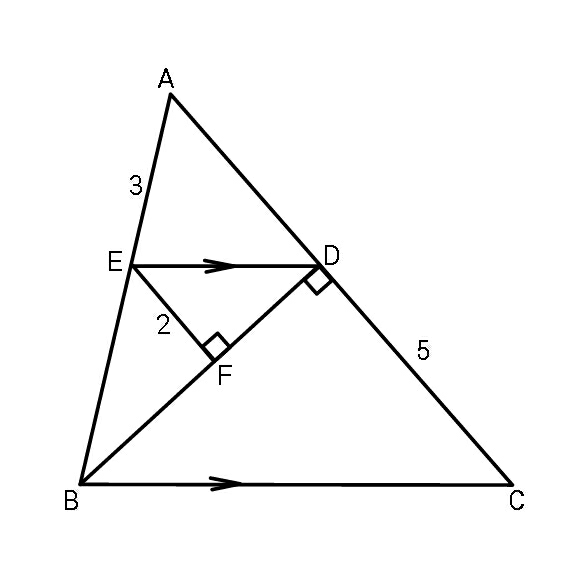
Question Number 70669 Answers: 0 Comments: 5

Question Number 70659 Answers: 1 Comments: 0
Question Number 70653 Answers: 1 Comments: 1
Question Number 70651 Answers: 0 Comments: 3
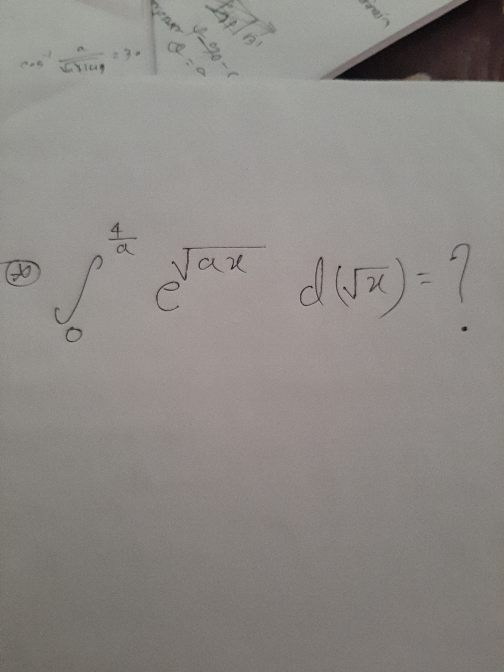
Question Number 70639 Answers: 0 Comments: 0

Question Number 70638 Answers: 1 Comments: 1

Question Number 70627 Answers: 0 Comments: 0
Question Number 70620 Answers: 0 Comments: 4

Question Number 70617 Answers: 1 Comments: 0
Question Number 70602 Answers: 0 Comments: 1
Question Number 70601 Answers: 1 Comments: 0
Question Number 70598 Answers: 1 Comments: 0
Question Number 70597 Answers: 4 Comments: 0
Question Number 70596 Answers: 1 Comments: 1
Question Number 70595 Answers: 0 Comments: 1
Question Number 70594 Answers: 1 Comments: 1
Pg 1415 Pg 1416 Pg 1417 Pg 1418 Pg 1419 Pg 1420 Pg 1421 Pg 1422 Pg 1423 Pg 1424
