
AllQuestion and Answers: Page 1418
Question Number 71052 Answers: 0 Comments: 2

Question Number 71051 Answers: 0 Comments: 2

Question Number 71050 Answers: 1 Comments: 1

Question Number 71049 Answers: 0 Comments: 2

Question Number 71047 Answers: 0 Comments: 1
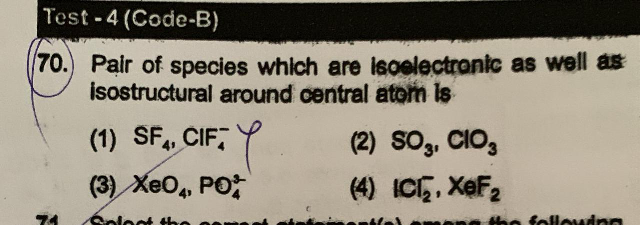
Question Number 71046 Answers: 0 Comments: 1
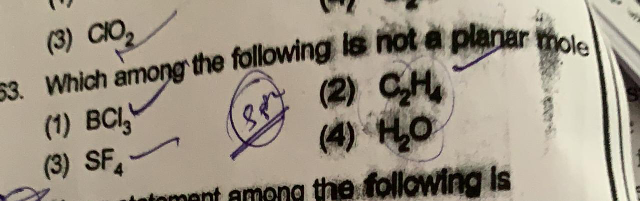
Question Number 71045 Answers: 0 Comments: 1
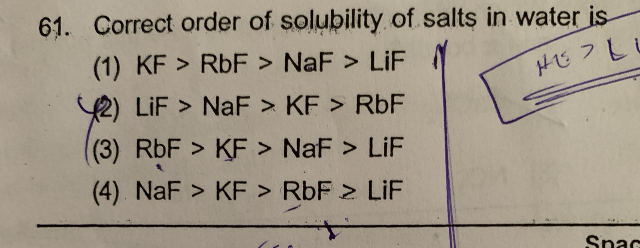
Question Number 71034 Answers: 0 Comments: 6

Question Number 71016 Answers: 2 Comments: 0
Question Number 71014 Answers: 0 Comments: 0
Question Number 71000 Answers: 0 Comments: 1
Question Number 70997 Answers: 1 Comments: 0

Question Number 70996 Answers: 0 Comments: 2

Question Number 70980 Answers: 0 Comments: 0
Question Number 70974 Answers: 0 Comments: 1
Question Number 70969 Answers: 1 Comments: 0

Question Number 70949 Answers: 1 Comments: 3
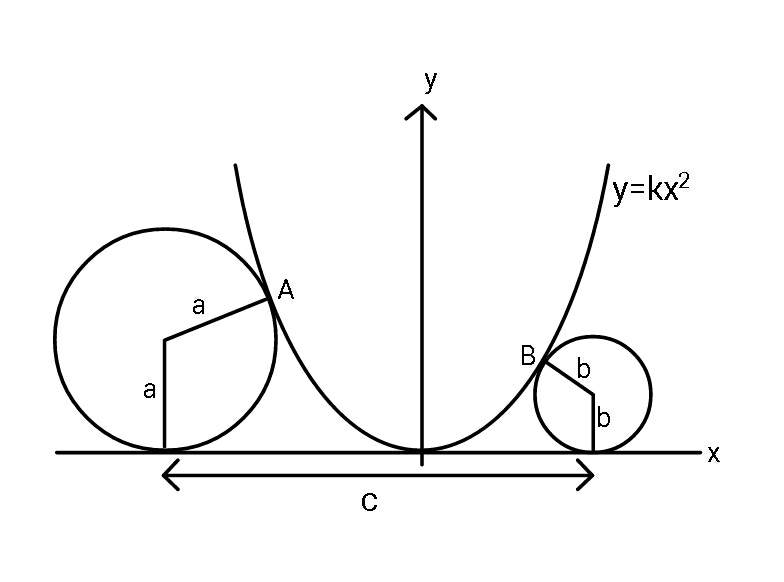
Question Number 70920 Answers: 1 Comments: 2
Question Number 70915 Answers: 1 Comments: 1

Question Number 70914 Answers: 2 Comments: 3
Question Number 70917 Answers: 1 Comments: 3
Question Number 70909 Answers: 1 Comments: 2

Question Number 70913 Answers: 1 Comments: 4

Question Number 70898 Answers: 2 Comments: 0
Question Number 70891 Answers: 0 Comments: 2
Question Number 70885 Answers: 1 Comments: 0
Pg 1413 Pg 1414 Pg 1415 Pg 1416 Pg 1417 Pg 1418 Pg 1419 Pg 1420 Pg 1421 Pg 1422
