Question and Answers Forum

AllQuestion and Answers: Page 1417

Question Number 66937 Answers: 1 Comments: 0

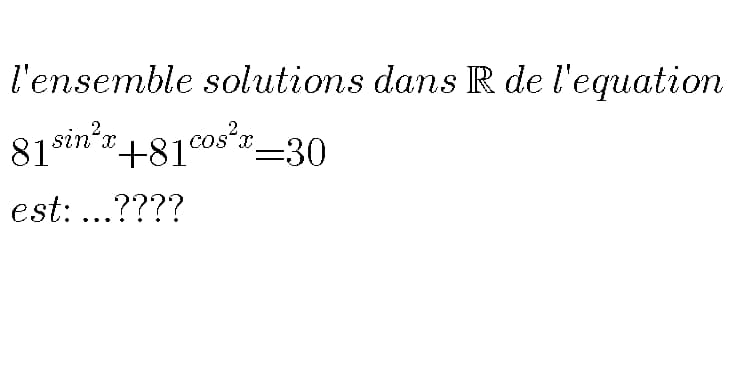
Question Number 66932 Answers: 1 Comments: 0

which of the sequences converges ? 1) a_n = n−(1/n) 2) a_n = ((−1)^n +1)(((n+1)/n))

$${which}\:{of}\:{the}\:{sequences}\:{converges}\:? \\ $$$$\left.\mathrm{1}\right)\:{a}_{{n}} =\:{n}−\frac{\mathrm{1}}{{n}} \\ $$$$\left.\mathrm{2}\right)\:{a}_{{n}} =\:\left(\left(−\mathrm{1}\right)^{{n}} +\mathrm{1}\right)\left(\frac{{n}+\mathrm{1}}{{n}}\right) \\ $$

Question Number 66928 Answers: 2 Comments: 0

(3^(120) /6^(60) ) express in your answer in 3 significant figure

$$\frac{\mathrm{3}^{\mathrm{120}} }{\mathrm{6}^{\mathrm{60}} } \\ $$$$\mathrm{express}\:\mathrm{in}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{in} \\ $$$$\mathrm{3}\:\mathrm{significant}\:\mathrm{figure} \\ $$

Question Number 66927 Answers: 0 Comments: 0

calcul la limite suivante: lim (((1^x +2^x +3^x +......+n^x )/n))^(1/x) =A x→0 trouve la valeur de A trouve la valeur de P definir par: P=(A/((((n! ))^(1/n) )^((n−1)) ))=???

$${calcul}\:{la}\:{limite}\:{suivante}: \\ $$$${lim}\:\:\:\:\:\:\:\left(\frac{\mathrm{1}^{{x}} +\mathrm{2}^{{x}} +\mathrm{3}^{{x}} +......+{n}^{{x}} }{{n}}\right)^{\frac{\mathrm{1}}{{x}}} =\mathrm{A} \\ $$$${x}\rightarrow\mathrm{0} \\ $$$$\mathrm{trouve}\:\mathrm{la}\:\mathrm{valeur}\:\mathrm{de}\:\boldsymbol{\mathrm{A}} \\ $$$$\mathrm{trouve}\:\mathrm{la}\:\mathrm{valeur}\:\mathrm{de}\:\boldsymbol{\mathrm{P}}\:\mathrm{definir}\:\mathrm{par}: \\ $$$$\boldsymbol{\mathrm{P}}=\frac{\boldsymbol{\mathrm{A}}}{\left(\sqrt[{\mathrm{n}}]{\mathrm{n}!\:}\right)^{\left(\mathrm{n}−\mathrm{1}\right)} }=??? \\ $$

Question Number 66922 Answers: 0 Comments: 1

Question Number 66910 Answers: 0 Comments: 1

P = Σ_(n=1) ^(999) (1/((2n−1)(2n))) Q = Σ_(n=1) ^(999) (1/((999+n)(1999−n))) (P/Q) = ?

$${P}\:\:=\:\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{999}} {\sum}}\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}\right)} \\ $$$${Q}\:\:=\:\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{999}} {\sum}}\:\frac{\mathrm{1}}{\left(\mathrm{999}+{n}\right)\left(\mathrm{1999}−{n}\right)} \\ $$$$\frac{{P}}{{Q}}\:\:=\:\:? \\ $$

Question Number 66909 Answers: 0 Comments: 0

∫ (((√(x^(2019) +2019)) + ((x^(2018) +2018))^(1/3) )/(((x^(2017) +2017))^(1/4) + ((x^(2016) +2016))^(1/5) )) dx = ?

$$\int\:\:\frac{\sqrt{{x}^{\mathrm{2019}} +\mathrm{2019}}\:\:+\:\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2018}} +\mathrm{2018}}}{\sqrt[{\mathrm{4}}]{{x}^{\mathrm{2017}} +\mathrm{2017}}\:\:+\:\:\sqrt[{\mathrm{5}}]{{x}^{\mathrm{2016}} +\mathrm{2016}}}\:\:{dx}\:\:=\:\:? \\ $$

Question Number 66906 Answers: 1 Comments: 5

Intergrate I=∫ (t^2 /(1+t^4 )) dt

$${Intergrate}\:{I}=\int\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }\:{dt} \\ $$

Question Number 66895 Answers: 1 Comments: 0

x+y+z=−B xy+yz+zx=C xyz=−D find x,y and z in terms of B,C and D

$${x}+{y}+{z}=−{B} \\ $$$${xy}+{yz}+{zx}={C} \\ $$$${xyz}=−{D} \\ $$$${find}\:{x},{y}\:{and}\:{z}\:{in}\:{terms}\:{of}\:{B},{C}\:{and}\:{D} \\ $$

Question Number 66971 Answers: 0 Comments: 3

∫(dx/(x(√(x^2 +x+1 ))))=? please help

$$\int\frac{\mathrm{dx}}{\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\:}}=? \\ $$$$\boldsymbol{\mathrm{p}\mathfrak{l}}\mathrm{ease}\:\mathrm{help} \\ $$

Question Number 66969 Answers: 1 Comments: 1

Question Number 66968 Answers: 0 Comments: 0

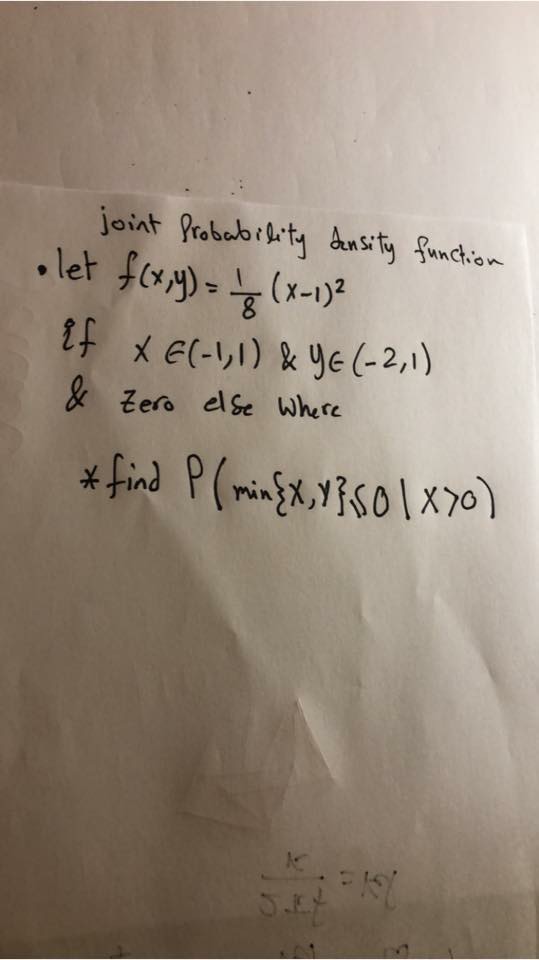
Question Number 66890 Answers: 3 Comments: 0

x^x + x^(2x) = 20 x^x = ?

$$\: \\ $$$$\:\:\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}} \:+\:\boldsymbol{\mathrm{x}}^{\mathrm{2}\boldsymbol{\mathrm{x}}} \:=\:\mathrm{20} \\ $$$$\: \\ $$$$\:\:\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}} \:=\:? \\ $$$$\: \\ $$

Question Number 66875 Answers: 0 Comments: 4

Question Number 66866 Answers: 1 Comments: 1

Question Number 66865 Answers: 1 Comments: 1

A and B are two towns 360km apart. An express bus departs from A at 8a.m and maintains an average speed of 90km/h between A and B. Another bus starts from B also at 8a.m and moves towards A making four stops at four equally spaced points between B and A. Each stop is of duration 5 minutes and the average speed between any two stops is 60km/h. Calculate the distance between the two buses at 10p.m.

$${A}\:{and}\:{B}\:{are}\:{two}\:{towns}\:\mathrm{360}{km}\:{apart}. \\ $$$${An}\:{express}\:{bus}\:{departs}\:{from}\:{A}\:{at} \\ $$$$\mathrm{8}{a}.{m}\:{and}\:{maintains}\:{an}\:{average} \\ $$$${speed}\:{of}\:\mathrm{90}{km}/{h}\:{between}\:{A}\:{and}\:{B}. \\ $$$${Another}\:{bus}\:{starts}\:{from}\:{B}\:{also}\:{at} \\ $$$$\mathrm{8}{a}.{m}\:{and}\:{moves}\:{towards}\:{A}\:{making} \\ $$$${four}\:{stops}\:{at}\:{four}\:{equally}\:{spaced} \\ $$$${points}\:{between}\:{B}\:{and}\:{A}.\:{Each}\:{stop} \\ $$$${is}\:{of}\:{duration}\:\mathrm{5}\:{minutes}\:{and}\:{the} \\ $$$${average}\:{speed}\:{between}\:{any}\:{two}\:{stops} \\ $$$${is}\:\mathrm{60}{km}/{h}.\:{Calculate}\:{the}\:{distance} \\ $$$${between}\:{the}\:{two}\:{buses}\:{at}\:\mathrm{10}{p}.{m}. \\ $$

Question Number 66868 Answers: 0 Comments: 3

A town N is 340km due west of town G and town K is due west of town N. A helicopter Zebra left G for K at 9a.m. Another helicopter Buffalo left N for K at 11a.m. Helicopter Buffalo travelled at an average speed of 20km/h faster than helicopter Zebra. If both helicopters reached K at 12.30p.m, find the speed of helicopter Buffalo.

$${A}\:{town}\:{N}\:{is}\:\mathrm{340}{km}\:{due}\:{west}\:{of}\: \\ $$$${town}\:{G}\:{and}\:{town}\:{K}\:{is}\:{due}\:{west}\: \\ $$$${of}\:{town}\:{N}.\:{A}\:{helicopter}\:{Zebra}\: \\ $$$${left}\:{G}\:{for}\:{K}\:{at}\:\mathrm{9}{a}.{m}.\:{Another}\: \\ $$$${helicopter}\:{Buffalo}\:{left}\:{N}\:{for}\:{K} \\ $$$${at}\:\mathrm{11}{a}.{m}.\:{Helicopter}\:{Buffalo} \\ $$$${travelled}\:{at}\:{an}\:{average}\:{speed}\:{of}\: \\ $$$$\mathrm{20}{km}/{h}\:{faster}\:{than}\:{helicopter} \\ $$$${Zebra}.\:{If}\:{both}\:{helicopters}\:{reached} \\ $$$${K}\:{at}\:\mathrm{12}.\mathrm{30}{p}.{m},\:{find}\:{the}\:{speed}\:{of}\: \\ $$$${helicopter}\:{Buffalo}. \\ $$

Question Number 66863 Answers: 0 Comments: 0

x^3 (b−x)^2 +aex(x−b)+e^2 =0 solve for x.

$$\:\:\:{x}^{\mathrm{3}} \left({b}−{x}\right)^{\mathrm{2}} +{aex}\left({x}−{b}\right)+{e}^{\mathrm{2}} =\mathrm{0}\: \\ $$$${solve}\:{for}\:{x}. \\ $$

Question Number 66862 Answers: 0 Comments: 1

lim_(x→0) 3x^5

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}3}{x}^{\mathrm{5}} \\ $$

Question Number 66857 Answers: 0 Comments: 3

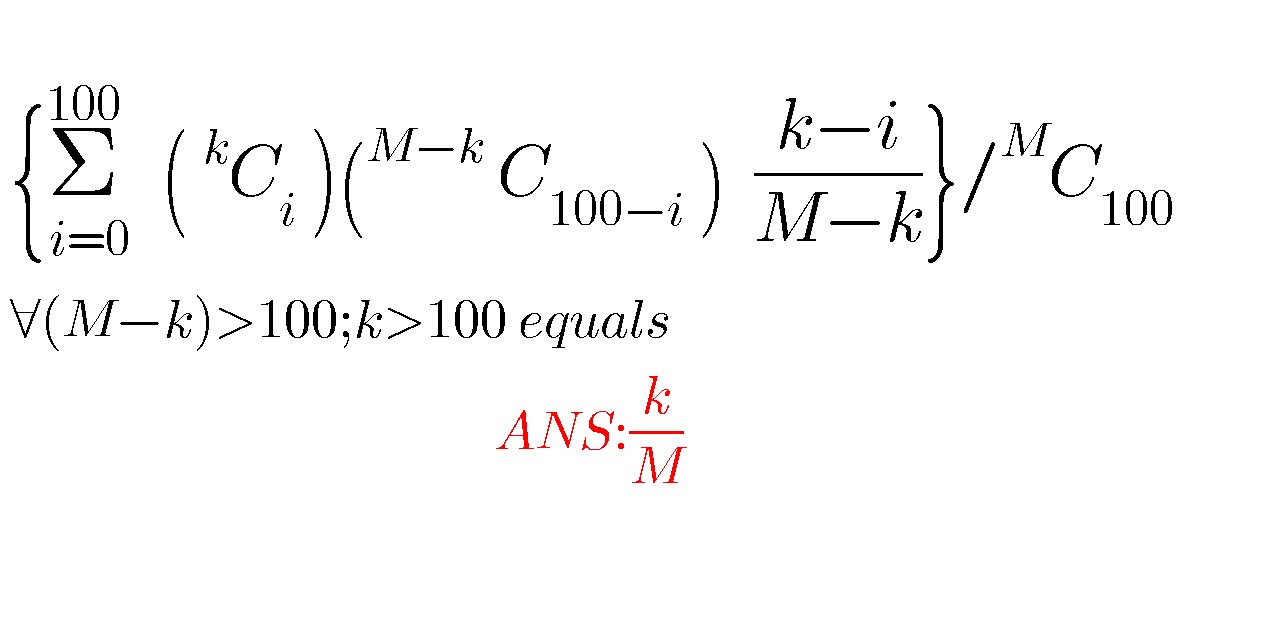
Question Number 66856 Answers: 1 Comments: 0

Two towns T and S are 300 km apart. Two buses A and B started from T at the same time travelling towards S. Bus B, travelling at an average speed of 10km/h greater than that of A reached S 1(1/4) hours earlier. (a) Find the average speed of A (b) How far was A from T when B reached S.

$${Two}\:{towns}\:{T}\:{and}\:{S}\:{are}\:\mathrm{300}\:{km}\:{apart}. \\ $$$${Two}\:{buses}\:{A}\:{and}\:{B}\:{started}\:{from} \\ $$$${T}\:{at}\:{the}\:{same}\:{time}\:{travelling}\:{towards} \\ $$$${S}.\:{Bus}\:{B},\:{travelling}\:{at}\:{an}\:{average} \\ $$$${speed}\:{of}\:\mathrm{10}{km}/{h}\:{greater}\:{than}\:{that} \\ $$$${of}\:{A}\:{reached}\:{S}\:\mathrm{1}\frac{\mathrm{1}}{\mathrm{4}}\:{hours}\:{earlier}. \\ $$$$\left({a}\right)\:{Find}\:{the}\:{average}\:{speed}\:{of}\:{A} \\ $$$$\left({b}\right)\:{How}\:{far}\:{was}\:{A}\:{from}\:{T}\:{when} \\ $$$${B}\:{reached}\:{S}. \\ $$

Question Number 66855 Answers: 2 Comments: 0

simplify ((p^2 +2pq+q^2 )/(p^3 −pq^2 +p^2 q−q^3 ))

$${simplify} \\ $$$$\frac{{p}^{\mathrm{2}} +\mathrm{2}{pq}+{q}^{\mathrm{2}} }{{p}^{\mathrm{3}} −{pq}^{\mathrm{2}} +{p}^{\mathrm{2}} {q}−{q}^{\mathrm{3}} } \\ $$

Question Number 66852 Answers: 0 Comments: 3

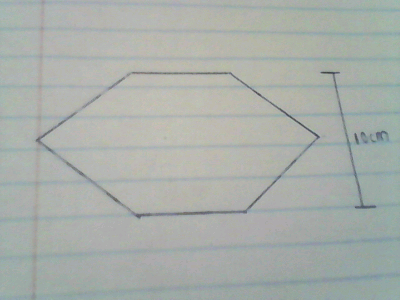
Question Number 66851 Answers: 2 Comments: 1

Question Number 66849 Answers: 0 Comments: 2

Question Number 66846 Answers: 0 Comments: 2

Pg 1412 Pg 1413 Pg 1414 Pg 1415 Pg 1416 Pg 1417 Pg 1418 Pg 1419 Pg 1420 Pg 1421

Contact: info@tinkutara.com