
AllQuestion and Answers: Page 1416
Question Number 71420 Answers: 0 Comments: 0

Question Number 71410 Answers: 1 Comments: 0
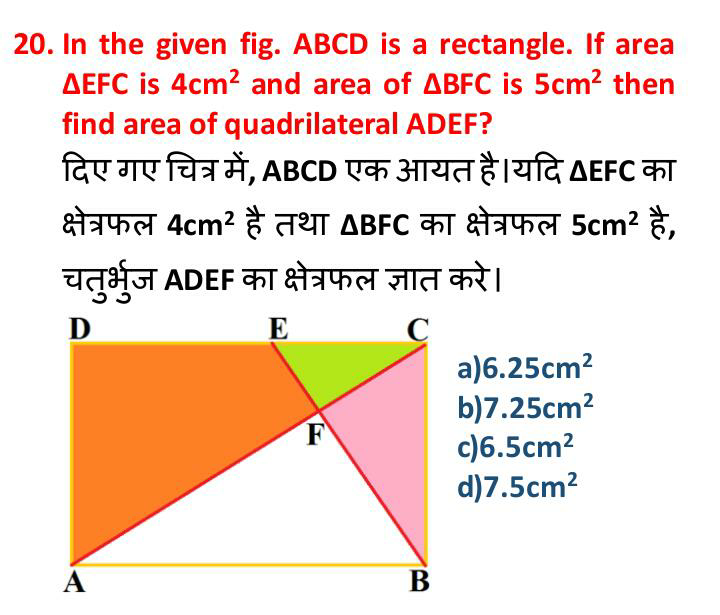
Question Number 71406 Answers: 0 Comments: 6
Question Number 71428 Answers: 1 Comments: 0

Question Number 71396 Answers: 0 Comments: 0

Question Number 71371 Answers: 0 Comments: 1

Question Number 71360 Answers: 0 Comments: 2
Question Number 71348 Answers: 0 Comments: 3

Question Number 71327 Answers: 2 Comments: 0
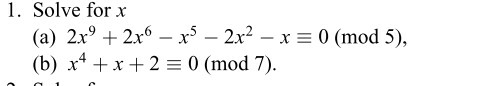
Question Number 71326 Answers: 2 Comments: 0
Question Number 71317 Answers: 1 Comments: 3
Question Number 71315 Answers: 0 Comments: 0
Question Number 71314 Answers: 2 Comments: 1
Question Number 71311 Answers: 1 Comments: 1

Question Number 71301 Answers: 0 Comments: 0
Question Number 71362 Answers: 0 Comments: 0
Question Number 71294 Answers: 1 Comments: 1
Question Number 71282 Answers: 4 Comments: 0
Question Number 71273 Answers: 0 Comments: 1

Question Number 71265 Answers: 0 Comments: 1
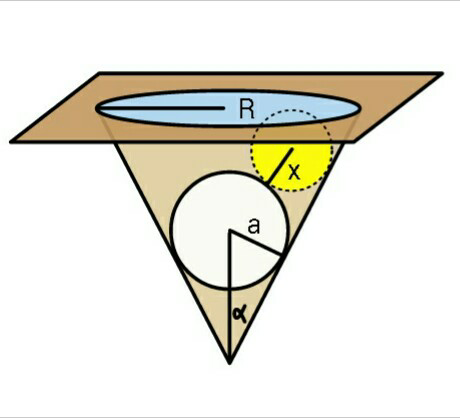
Question Number 71255 Answers: 1 Comments: 2
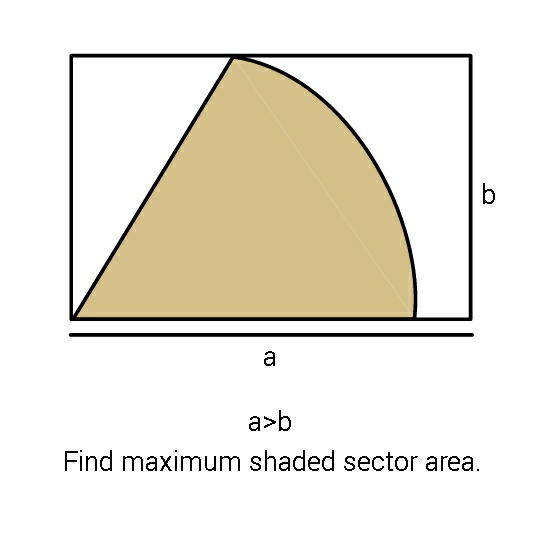
Question Number 71242 Answers: 3 Comments: 0
Question Number 71239 Answers: 2 Comments: 3
$$\int\frac{\mathrm{1}}{\mathrm{2cosx}−\mathrm{5sinx}−\mathrm{3}}\mathrm{dx} \\ $$
Question Number 71235 Answers: 2 Comments: 1
Question Number 71233 Answers: 1 Comments: 3

Question Number 71229 Answers: 0 Comments: 1

Pg 1411 Pg 1412 Pg 1413 Pg 1414 Pg 1415 Pg 1416 Pg 1417 Pg 1418 Pg 1419 Pg 1420
