
AllQuestion and Answers: Page 1415
Question Number 70909 Answers: 1 Comments: 2

Question Number 70913 Answers: 1 Comments: 4

Question Number 70898 Answers: 2 Comments: 0
Question Number 70891 Answers: 0 Comments: 2
Question Number 70885 Answers: 1 Comments: 0
Question Number 70876 Answers: 0 Comments: 0
Question Number 70874 Answers: 2 Comments: 0
Question Number 70873 Answers: 1 Comments: 0
Question Number 70872 Answers: 0 Comments: 1
Question Number 70871 Answers: 0 Comments: 1
Question Number 70887 Answers: 0 Comments: 2

Question Number 70865 Answers: 0 Comments: 2
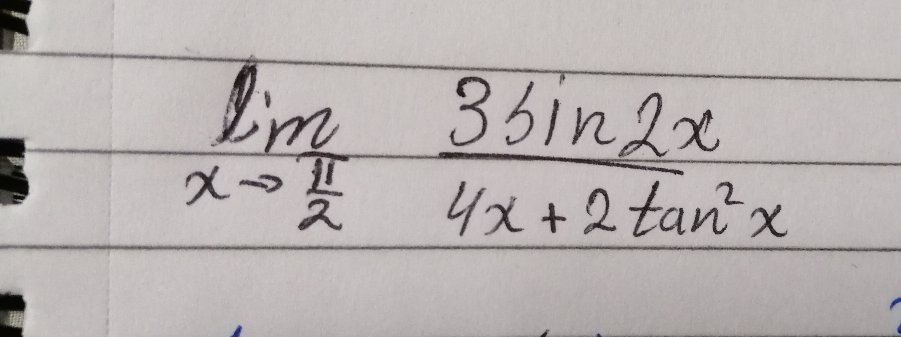
Question Number 70870 Answers: 0 Comments: 4
Question Number 70886 Answers: 2 Comments: 11

Question Number 70847 Answers: 2 Comments: 0
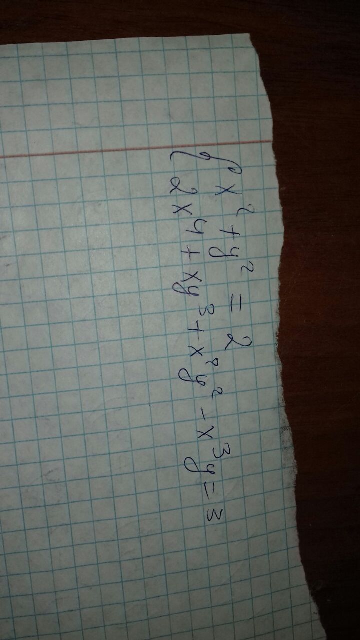
Question Number 70842 Answers: 0 Comments: 1

Question Number 70838 Answers: 1 Comments: 0
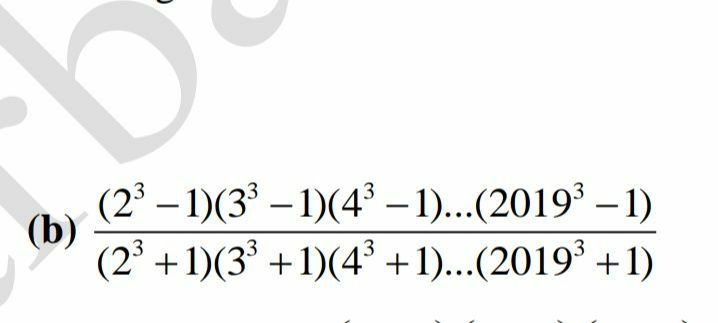
Question Number 70834 Answers: 1 Comments: 0
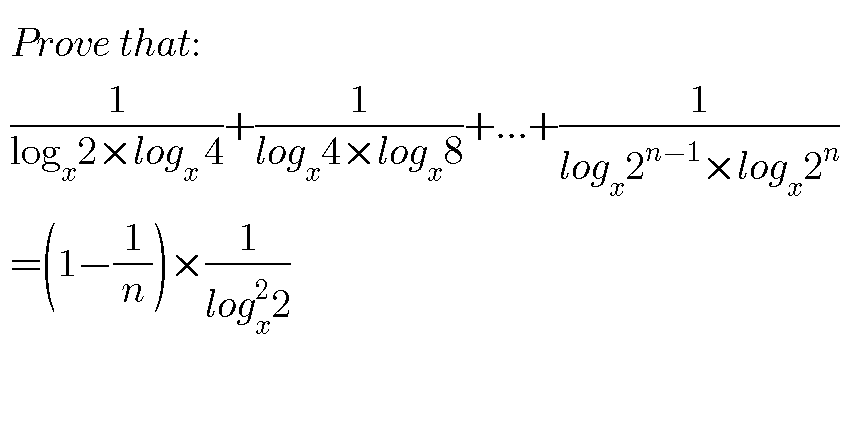
Question Number 70831 Answers: 2 Comments: 1

Question Number 70826 Answers: 2 Comments: 1
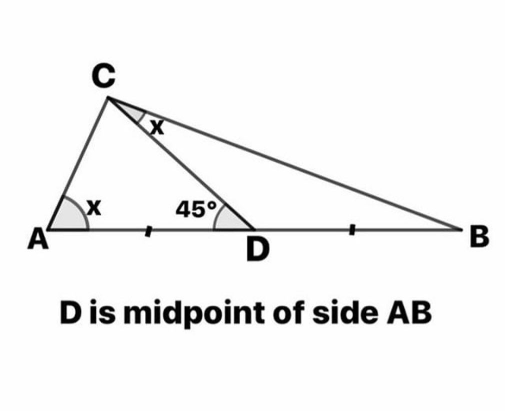
Question Number 70818 Answers: 1 Comments: 1
Question Number 70808 Answers: 1 Comments: 0
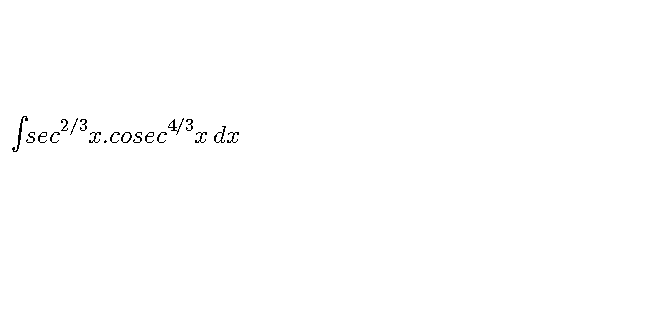
Question Number 70784 Answers: 1 Comments: 2

Question Number 70783 Answers: 1 Comments: 4
Question Number 70780 Answers: 0 Comments: 1
Question Number 70768 Answers: 1 Comments: 1

Pg 1410 Pg 1411 Pg 1412 Pg 1413 Pg 1414 Pg 1415 Pg 1416 Pg 1417 Pg 1418 Pg 1419
