Question and Answers Forum

AllQuestion and Answers: Page 1414

Question Number 67116 Answers: 4 Comments: 1

Question Number 67108 Answers: 2 Comments: 2

Three school children share some oranges as follows: Akwasi gets (1/3) of the total and the remainder is shared between Abena and Juana in the ratio 2: 3 . If Abena gets 24 oranges , how many does Akwasi get.

$$\mathrm{Three}\:\mathrm{school}\:\mathrm{children}\:\mathrm{share}\:\mathrm{some}\: \\ $$$$\mathrm{oranges}\:\mathrm{as}\:\mathrm{follows}:\:\mathrm{Akwasi}\:\mathrm{gets}\:\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{total}\:\mathrm{and}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{shared} \\ $$$$\mathrm{between}\:\mathrm{Abena}\:\mathrm{and}\:\mathrm{Juana}\:\mathrm{in}\:\mathrm{the}\:\mathrm{ratio} \\ $$$$\mathrm{2}:\:\mathrm{3}\:.\:\mathrm{If}\:\mathrm{Abena}\:\mathrm{gets}\:\mathrm{24}\:\mathrm{oranges}\:,\:\mathrm{how} \\ $$$$\mathrm{many}\:\mathrm{does}\:\mathrm{Akwasi}\:\mathrm{get}. \\ $$

Question Number 67106 Answers: 0 Comments: 1

find the area abounded y=(√x) afind y=x−2?

$${find}\:{the}\:{area}\:{abounded}\:{y}=\sqrt{{x}} \\ $$$${afind}\:{y}={x}−\mathrm{2}? \\ $$

Question Number 67105 Answers: 0 Comments: 0

find the area abounded y=(√x) afind y=x−2?

$${find}\:{the}\:{area}\:{abounded}\:{y}=\sqrt{{x}} \\ $$$${afind}\:{y}={x}−\mathrm{2}? \\ $$

Question Number 67102 Answers: 2 Comments: 0

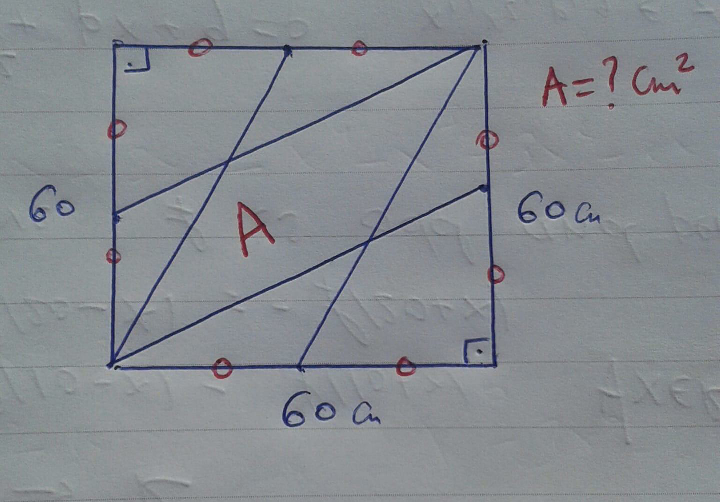
Question Number 67083 Answers: 1 Comments: 0

CosA+CosB+CosC=1+4Cos(((B+C)/2)).Cos(((C+A)/2)).Cos(((A+B)/2))=1+4Cos(((Π−A)/4)).Cos(((Π−B)/4)).Cos(((Π−C)/4)) prove that if A+B+C=Π

$$\mathrm{CosA}+\mathrm{CosB}+\mathrm{CosC}=\mathrm{1}+\mathrm{4Cos}\left(\frac{\mathrm{B}+\mathrm{C}}{\mathrm{2}}\right).\mathrm{Cos}\left(\frac{\mathrm{C}+\mathrm{A}}{\mathrm{2}}\right).\mathrm{Cos}\left(\frac{\mathrm{A}+\mathrm{B}}{\mathrm{2}}\right)=\mathrm{1}+\mathrm{4Cos}\left(\frac{\Pi−\mathrm{A}}{\mathrm{4}}\right).\mathrm{Cos}\left(\frac{\Pi−\mathrm{B}}{\mathrm{4}}\right).\mathrm{Cos}\left(\frac{\Pi−\mathrm{C}}{\mathrm{4}}\right) \\ $$$$\mathrm{prove}\:\mathrm{that}\:\mathrm{if}\:\mathrm{A}+\mathrm{B}+\mathrm{C}=\Pi \\ $$

Question Number 67072 Answers: 1 Comments: 0

Question Number 67071 Answers: 0 Comments: 7

Question Number 67070 Answers: 0 Comments: 3

Question Number 67069 Answers: 0 Comments: 1

Question Number 67059 Answers: 0 Comments: 1

find the area abounded y=(√(x−2)) and y=x−2 ?

$${find}\:{the}\:{area}\:{abounded}\:{y}=\sqrt{{x}−\mathrm{2}} \\ $$$${and}\:{y}={x}−\mathrm{2}\:? \\ $$

Question Number 67058 Answers: 0 Comments: 0

find the area abounded y=(√(x−2)) and y=x−2 ?

$${find}\:{the}\:{area}\:{abounded}\:{y}=\sqrt{{x}−\mathrm{2}} \\ $$$${and}\:{y}={x}−\mathrm{2}\:? \\ $$

Question Number 67057 Answers: 1 Comments: 0

(1)find ∩_(n=1) ^∞ [0, (1/n)) (2)find ∪_(n=2) ^∞ [(1/n), 1−(1/n)]

$$\left(\mathrm{1}\right){find}\:\cap_{{n}=\mathrm{1}} ^{\infty} \left[\mathrm{0},\:\frac{\mathrm{1}}{{n}}\right) \\ $$$$\left(\mathrm{2}\right){find}\:\cup_{{n}=\mathrm{2}} ^{\infty} \left[\frac{\mathrm{1}}{{n}},\:\mathrm{1}−\frac{\mathrm{1}}{{n}}\right] \\ $$

Question Number 67055 Answers: 0 Comments: 0

let Z_+ =N∪{0}, f: Z_+ ×Z_+ →Z_+ f(m, n)=(((m+n)(m+n+1))/2)+m prove that f is a one-to-one function and also an onto function

$${let}\:\mathbb{Z}_{+} =\mathbb{N}\cup\left\{\mathrm{0}\right\},\:{f}:\:\mathbb{Z}_{+} ×\mathbb{Z}_{+} \rightarrow\mathbb{Z}_{+} \\ $$$${f}\left({m},\:{n}\right)=\frac{\left({m}+{n}\right)\left({m}+{n}+\mathrm{1}\right)}{\mathrm{2}}+{m} \\ $$$${prove}\:{that}\:{f}\:{is}\:{a}\:{one}-{to}-{one}\:{function} \\ $$$${and}\:{also}\:{an}\:{onto}\:{function} \\ $$

Question Number 67038 Answers: 1 Comments: 1

calculate ∫_(−1) ^1 (x^(2n) /(1+2^(sinx) ))dx with n integr.

$${calculate}\:\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{{x}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{sinx}} }{dx}\:\:\:{with}\:{n}\:{integr}. \\ $$

Question Number 67035 Answers: 1 Comments: 2

Question Number 67034 Answers: 0 Comments: 2

calculate Σ_(n=1) ^∞ ((cos(2nx))/n)

$${calculate}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left(\mathrm{2}{nx}\right)}{{n}} \\ $$

Question Number 67033 Answers: 0 Comments: 5

Question Number 67032 Answers: 0 Comments: 0

Question Number 67031 Answers: 0 Comments: 4

lim_(x→−1) ((((x^5 )^(1/7) +1)/(1+(x^7 )^(1/(9 )) )))^(1/3) =?

$$\: \\ $$$$\:\underset{\boldsymbol{\mathrm{x}}\rightarrow−\mathrm{1}} {\boldsymbol{\mathrm{lim}}}\sqrt[{\mathrm{3}}]{\frac{\sqrt[{\mathrm{7}}]{\boldsymbol{\mathrm{x}}^{\mathrm{5}} }+\mathrm{1}}{\mathrm{1}+\sqrt[{\mathrm{9}\:}]{\boldsymbol{\mathrm{x}}^{\mathrm{7}} }}}=? \\ $$$$\: \\ $$

Question Number 67026 Answers: 0 Comments: 5

Question Number 67025 Answers: 0 Comments: 3

Question Number 67023 Answers: 1 Comments: 1

find the sequence U_n wich verify U_n +U_(n+1) =sin(n) ∀n from n

$${find}\:{the}\:{sequence}\:{U}_{{n}} \:{wich}\:{verify}\:\:{U}_{{n}} +{U}_{{n}+\mathrm{1}} ={sin}\left({n}\right)\:\:\forall{n}\:{from}\:{n} \\ $$

Question Number 67022 Answers: 0 Comments: 0

find ∫ (1+(√x))(√(x^2 +3))dx

$${find}\:\int\:\left(\mathrm{1}+\sqrt{{x}}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}{dx} \\ $$

Question Number 67021 Answers: 0 Comments: 1

find f(x) =∫_0 ^1 ln(x +e^(−t) )dt with x>0

$${find}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\:+{e}^{−{t}} \right){dt}\:\:\:{with}\:{x}>\mathrm{0} \\ $$

Question Number 67020 Answers: 0 Comments: 1

find f(x) = ∫_0 ^1 arctan(1+xt)dt with x real

$${find}\:{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctan}\left(\mathrm{1}+{xt}\right){dt}\:\:{with}\:{x}\:{real} \\ $$

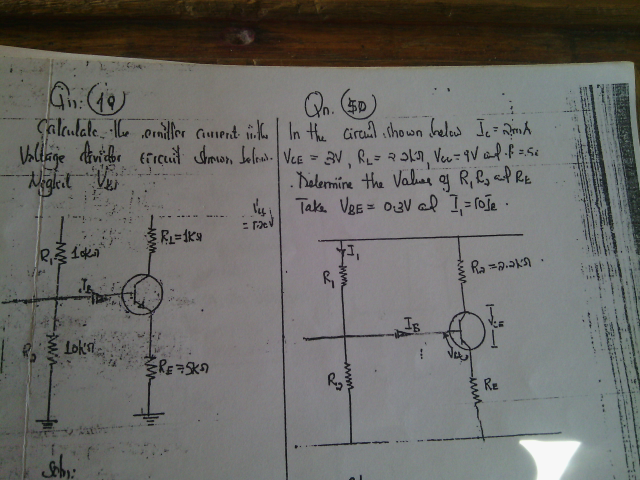
Pg 1409 Pg 1410 Pg 1411 Pg 1412 Pg 1413 Pg 1414 Pg 1415 Pg 1416 Pg 1417 Pg 1418

Contact: info@tinkutara.com