Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1413

Question Number 71196 Answers: 1 Comments: 0

the curve y = f(x), when f(x) is a quadratic expression has a maximum value point at (1,4). The curve touches the line 6x + y = 13. Find the value of x for which y = 8

$${the}\:{curve}\:{y}\:=\:{f}\left({x}\right),\:{when}\:{f}\left({x}\right)\:{is}\:{a}\:{quadratic}\:{expression}\:{has}\: \\ $$$${a}\:{maximum}\:{value}\:{point}\:{at}\:\left(\mathrm{1},\mathrm{4}\right).\:{The}\:{curve}\:{touches}\:{the}\:{line} \\ $$$$\mathrm{6}{x}\:+\:{y}\:=\:\mathrm{13}.\:{Find}\:{the}\:{value}\:{of}\:{x}\:{for}\:{which}\:{y}\:=\:\mathrm{8} \\ $$

Question Number 71184 Answers: 1 Comments: 4

Question Number 71198 Answers: 0 Comments: 0

A particle P is projected from a point O at the edge of a cliff 60m from the sea with a velocity of 30ms^(−1) . When P is at a point B where OB is a horizontal, another particle Qsuch that P and Q hit the sea simultaneously at thesame point A. Gven that they strike the sea 6seconds after P was fired ^ calculate a) the sine of the angle of elevation of projection. b) the distance from A to O. c) the time of flight of Q. d) the Range . (take g = 10ms^(−2) ) please help

$${A}\:{particle}\:{P}\:{is}\:{projected}\:{from}\:\:{a}\:{point}\:{O}\:{at}\:\:{the}\:{edge}\:{of}\:{a}\:{cliff}\:\mathrm{60}{m} \\ $$$${from}\:{the}\:{sea}\:{with}\:{a}\:{velocity}\:{of}\:\mathrm{30}{ms}^{−\mathrm{1}} .\:{When}\:{P}\:{is}\:{at}\:{a}\:{point}\:{B} \\ $$$${where}\:{OB}\:{is}\:{a}\:{horizontal},\:{another}\:{particle}\:{Qsuch}\:{that}\: \\ $$$${P}\:{and}\:{Q}\:{hit}\:{the}\:{sea}\:{simultaneously}\:{at}\:{thesame}\:{point}\:{A}.\:{Gven}\:{that}\:{they} \\ $$$${strike}\:{the}\:{sea}\:\mathrm{6}{seconds}\:{after}\:{P}\:{was}\:{fired}\bar {\:}\:{calculate} \\ $$$$\left.{a}\right)\:{the}\:{sine}\:{of}\:{the}\:{angle}\:{of}\:{elevation}\:{of}\:{projection}. \\ $$$$\left.{b}\right)\:{the}\:{distance}\:{from}\:{A}\:{to}\:{O}. \\ $$$$\left.{c}\right)\:{the}\:{time}\:{of}\:{flight}\:{of}\:{Q}. \\ $$$$\left.{d}\right)\:{the}\:{Range}\:. \\ $$$$\left({take}\:{g}\:=\:\mathrm{10}{ms}^{−\mathrm{2}} \right)\: \\ $$$${please}\:{help}\: \\ $$

Question Number 71197 Answers: 0 Comments: 0

Question Number 71175 Answers: 1 Comments: 3

∫(1/(x^2 +2016x))dx

$$\int\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{2016x}}\mathrm{dx} \\ $$

Question Number 71172 Answers: 0 Comments: 2

find fhe range f(x)=(4/(1+(√x)))

$${find}\:{fhe}\:{range} \\ $$$$ \\ $$$${f}\left({x}\right)=\frac{\mathrm{4}}{\mathrm{1}+\sqrt{{x}}} \\ $$

Question Number 71149 Answers: 1 Comments: 4

Question Number 71147 Answers: 2 Comments: 1

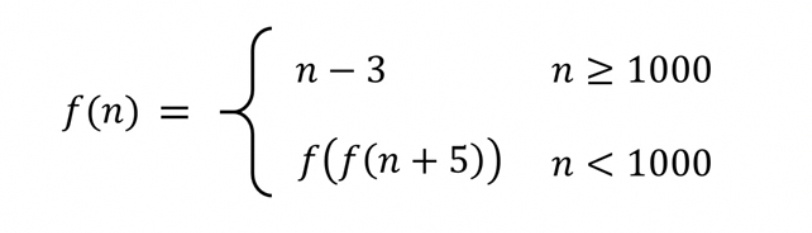
Question Number 71146 Answers: 1 Comments: 1

sin α=((12)/(13)) and α is in the 2nd quadrent. prove cos α=−(5/(13))

$$\mathrm{sin}\:\alpha=\frac{\mathrm{12}}{\mathrm{13}}\:\:\mathrm{and}\:\alpha\:\mathrm{is}\:\mathrm{in}\:\mathrm{the}\:\mathrm{2nd}\:\mathrm{quadrent}. \\ $$$$\mathrm{prove}\:\mathrm{cos}\:\alpha=−\frac{\mathrm{5}}{\mathrm{13}} \\ $$

Question Number 71143 Answers: 0 Comments: 1

let A_n =Σ_(k=0) ^n (1/(3k+1)) calculate A_n interms H_n =Σ_(k=1) ^n (1/k)

$${let}\:\:{A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{3}{k}+\mathrm{1}}\:{calculate}\:{A}_{{n}} \:{interms}\:{H}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}} \\ $$

Question Number 71142 Answers: 0 Comments: 1

find ∫(√(x(x+1)(x+2)))dx

$${find}\:\int\sqrt{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)}{dx} \\ $$

Question Number 71141 Answers: 0 Comments: 6

(2x)^x =(1/(16))

$$\left(\mathrm{2}{x}\right)^{{x}} =\frac{\mathrm{1}}{\mathrm{16}} \\ $$

Question Number 71134 Answers: 1 Comments: 0

if a, b and c are positive, find: ((a/b))^(log_(10) c) ×((b/c))^(log_(10) a) ×((c/a))^(log_(10) b)

$${if}\:{a},\:{b}\:{and}\:{c}\:{are}\:{positive},\:{find}: \\ $$$$\left(\frac{{a}}{{b}}\right)^{{log}_{\mathrm{10}} {c}} ×\left(\frac{{b}}{{c}}\right)^{{log}_{\mathrm{10}} {a}} ×\left(\frac{{c}}{{a}}\right)^{{log}_{\mathrm{10}} {b}} \\ $$$$ \\ $$

Question Number 71117 Answers: 0 Comments: 0

Question Number 71114 Answers: 0 Comments: 0

Question Number 71096 Answers: 1 Comments: 0

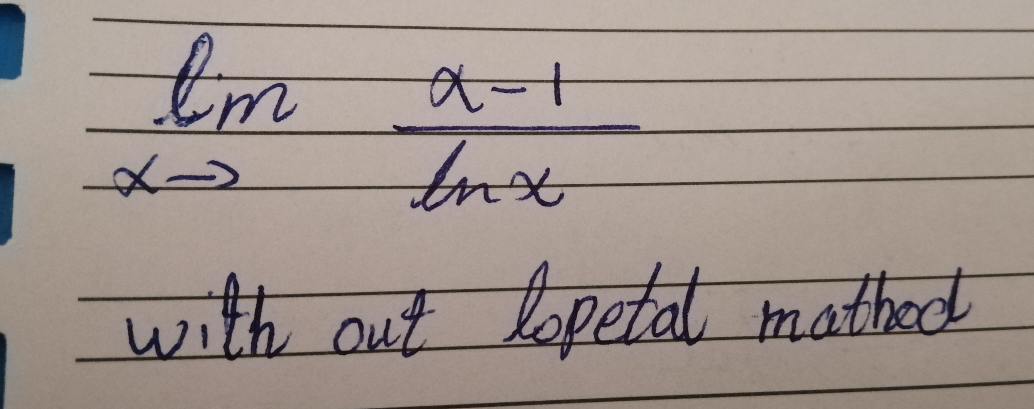
Question Number 71091 Answers: 0 Comments: 3

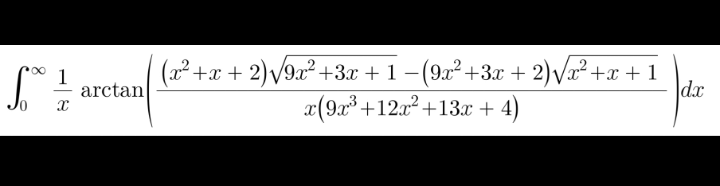
Question Number 71115 Answers: 1 Comments: 0

Question Number 71089 Answers: 1 Comments: 0

((√((√2)−1)))^x +((√((√2)+1)))^x =4

$$\left(\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\right)^{\mathrm{x}} +\left(\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}\right)^{\mathrm{x}} =\mathrm{4} \\ $$

Question Number 71082 Answers: 2 Comments: 0

prove that ∣ (√(∣x∣)) − (√(∣y∣)) ∣ ≤ (√(∣x−y∣))

$${prove}\:{that}\: \\ $$$$ \\ $$$$\mid\:\sqrt{\mid{x}\mid}\:−\:\sqrt{\mid{y}\mid}\:\mid\:\leqslant\:\sqrt{\mid{x}−{y}\mid}\: \\ $$$$ \\ $$

Question Number 71073 Answers: 3 Comments: 4

Question Number 71054 Answers: 0 Comments: 2

Question Number 71053 Answers: 1 Comments: 1

Question Number 71052 Answers: 0 Comments: 2

Question Number 71051 Answers: 0 Comments: 2

Question Number 71050 Answers: 1 Comments: 1

Pg 1408 Pg 1409 Pg 1410 Pg 1411 Pg 1412 Pg 1413 Pg 1414 Pg 1415 Pg 1416 Pg 1417

Terms of Service

Contact: info@tinkutara.com