
AllQuestion and Answers: Page 1412
Question Number 71448 Answers: 0 Comments: 1
Question Number 71673 Answers: 1 Comments: 1

Question Number 71439 Answers: 1 Comments: 1
Question Number 71432 Answers: 0 Comments: 2
Question Number 71423 Answers: 0 Comments: 7

Question Number 71421 Answers: 1 Comments: 1

Question Number 71420 Answers: 0 Comments: 0

Question Number 71410 Answers: 1 Comments: 0
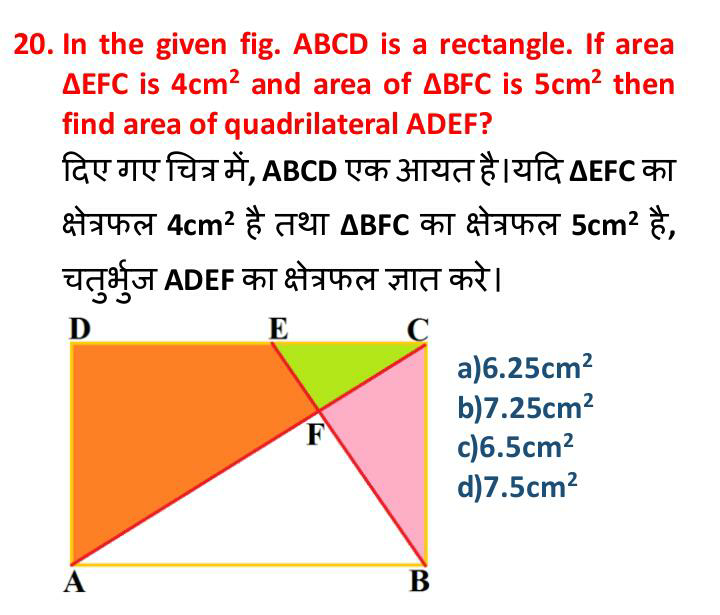
Question Number 71406 Answers: 0 Comments: 6
Question Number 71428 Answers: 1 Comments: 0

Question Number 71396 Answers: 0 Comments: 0

Question Number 71371 Answers: 0 Comments: 1

Question Number 71360 Answers: 0 Comments: 2
Question Number 71348 Answers: 0 Comments: 3

Question Number 71327 Answers: 2 Comments: 0
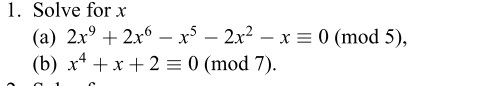
Question Number 71326 Answers: 2 Comments: 0
Question Number 71317 Answers: 1 Comments: 3
Question Number 71315 Answers: 0 Comments: 0
Question Number 71314 Answers: 2 Comments: 1
Question Number 71311 Answers: 1 Comments: 1

Question Number 71301 Answers: 0 Comments: 0
Question Number 71362 Answers: 0 Comments: 0
Question Number 71294 Answers: 1 Comments: 1
Question Number 71282 Answers: 4 Comments: 0
Question Number 71273 Answers: 0 Comments: 1

Question Number 71265 Answers: 0 Comments: 1
Pg 1407 Pg 1408 Pg 1409 Pg 1410 Pg 1411 Pg 1412 Pg 1413 Pg 1414 Pg 1415 Pg 1416
