
AllQuestion and Answers: Page 1410
Question Number 72316 Answers: 0 Comments: 6
Question Number 72359 Answers: 1 Comments: 2

Question Number 72296 Answers: 1 Comments: 4
Question Number 72294 Answers: 1 Comments: 4

Question Number 72291 Answers: 1 Comments: 0
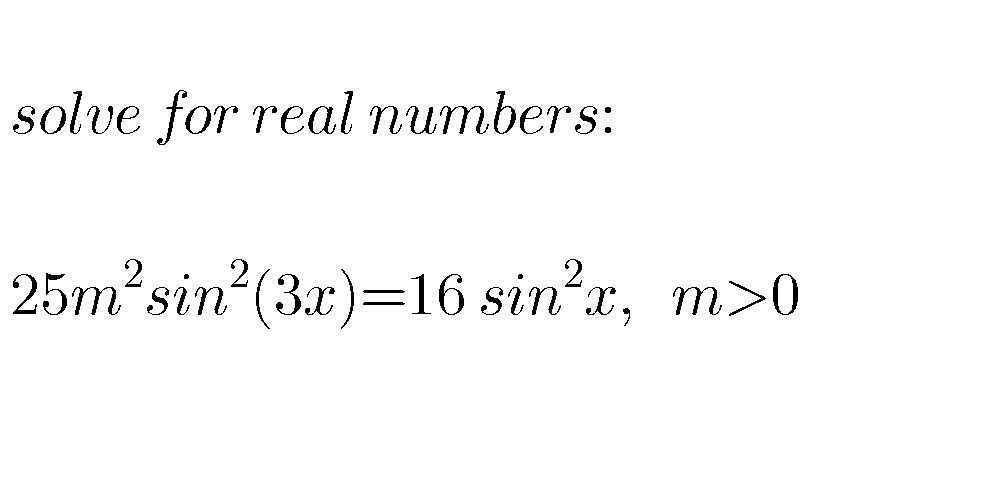
Question Number 72289 Answers: 2 Comments: 0
Question Number 72275 Answers: 0 Comments: 2
Question Number 72260 Answers: 1 Comments: 3
Question Number 72259 Answers: 1 Comments: 0
$$\int{yz}\:{dx}\:+\int{xz}\:{dy}\:+\int{xy}\:{dz}\:\:\:\:{pleas}\:{sir}\:{help}\:{me}\:? \\ $$
Question Number 72286 Answers: 0 Comments: 0

Question Number 72247 Answers: 1 Comments: 0

Question Number 72232 Answers: 0 Comments: 6
Question Number 72251 Answers: 0 Comments: 1

Question Number 72250 Answers: 0 Comments: 2
Question Number 72248 Answers: 1 Comments: 1

Question Number 72287 Answers: 0 Comments: 0

Question Number 72218 Answers: 0 Comments: 3

Question Number 72198 Answers: 1 Comments: 8
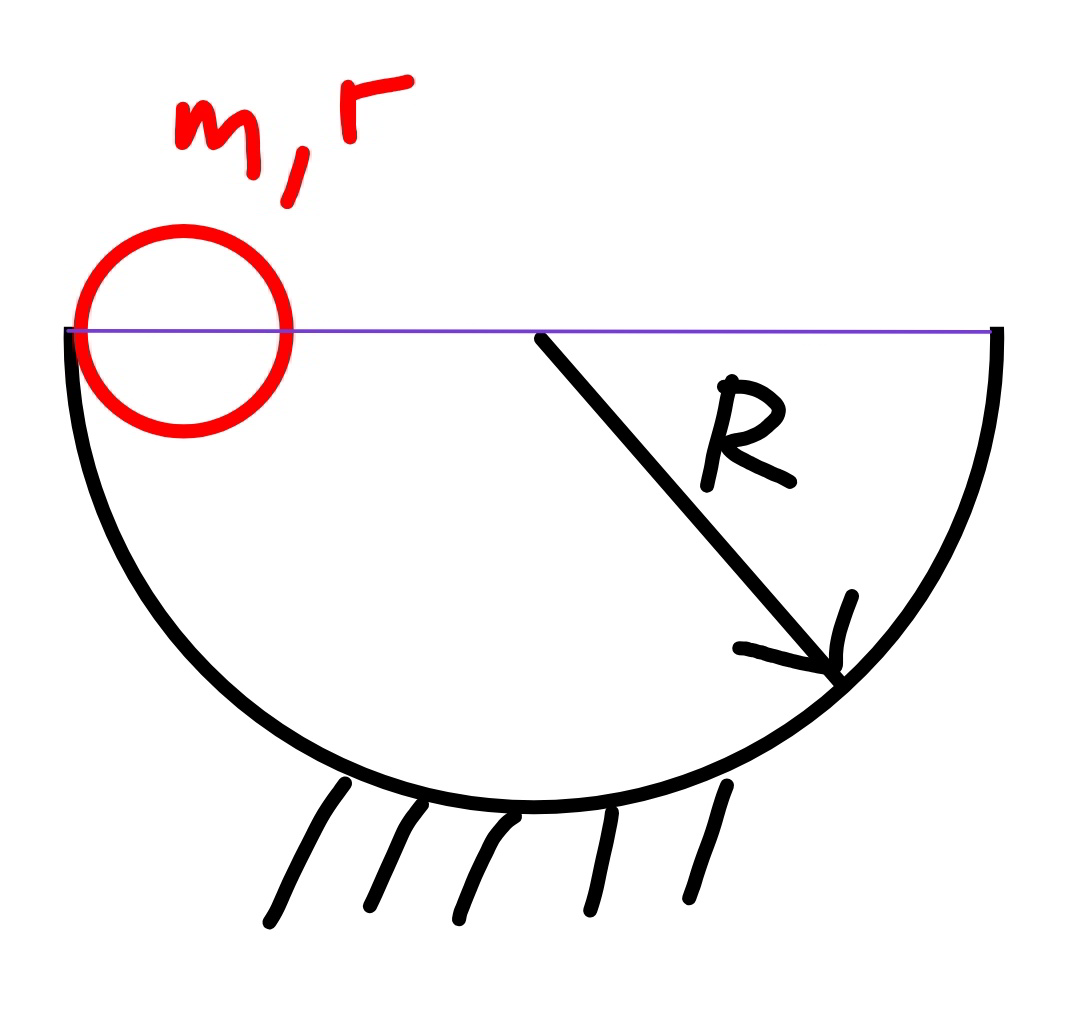
Question Number 72194 Answers: 2 Comments: 1
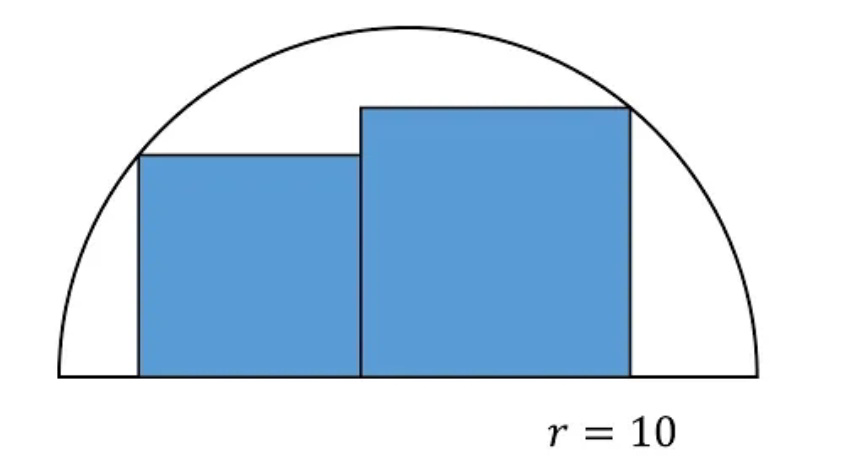
Question Number 72190 Answers: 1 Comments: 2
$$\mathrm{3}^{\mathrm{x}} +\mathrm{4}^{\mathrm{x}} =\mathrm{5}^{\mathrm{x}} \\ $$
Question Number 72185 Answers: 0 Comments: 2

Question Number 72390 Answers: 0 Comments: 1
Question Number 72389 Answers: 1 Comments: 0
Question Number 72161 Answers: 1 Comments: 4
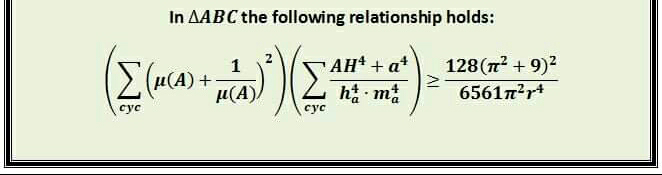
Question Number 72178 Answers: 0 Comments: 3
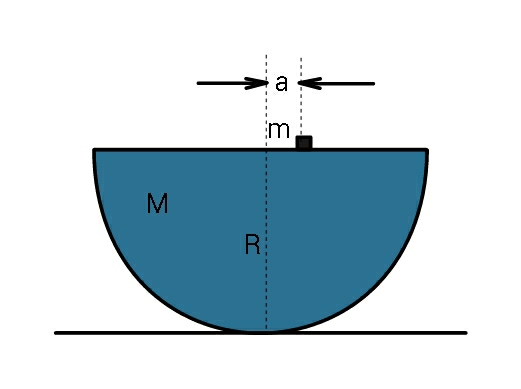
Question Number 72153 Answers: 1 Comments: 3
Pg 1405 Pg 1406 Pg 1407 Pg 1408 Pg 1409 Pg 1410 Pg 1411 Pg 1412 Pg 1413 Pg 1414
