
AllQuestion and Answers: Page 1409
Question Number 72421 Answers: 1 Comments: 0

Question Number 72416 Answers: 0 Comments: 1

Question Number 72414 Answers: 1 Comments: 1

Question Number 72413 Answers: 0 Comments: 0
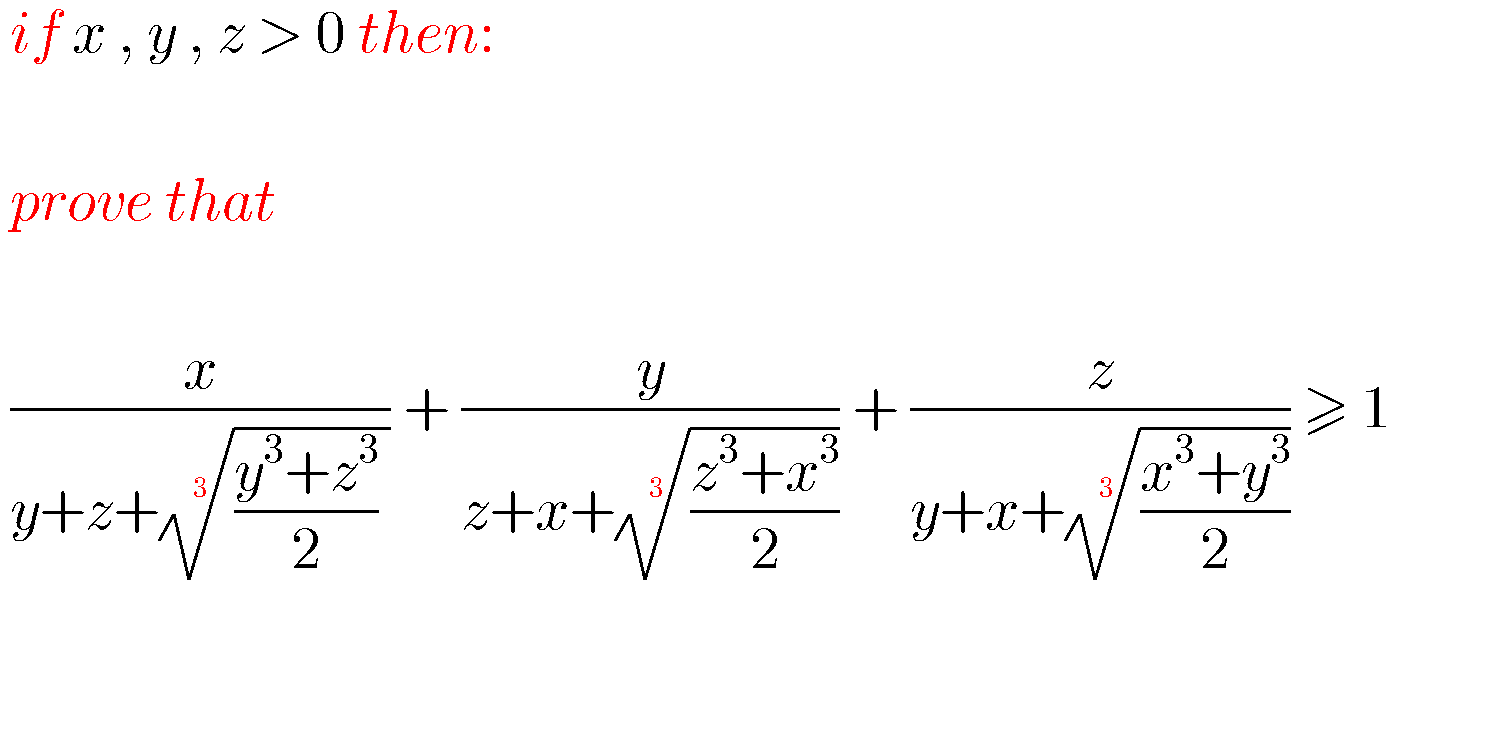
Question Number 72408 Answers: 1 Comments: 1

Question Number 72401 Answers: 1 Comments: 0
Question Number 72398 Answers: 0 Comments: 4
Question Number 72397 Answers: 0 Comments: 4
Question Number 72396 Answers: 0 Comments: 2
Question Number 72395 Answers: 0 Comments: 0
$${find}\:\sum_{{k}=\mathrm{0}} ^{{n}} \left({C}_{{n}} ^{{k}} \right)^{\mathrm{3}} \\ $$
Question Number 72394 Answers: 0 Comments: 3
Question Number 72393 Answers: 0 Comments: 0
Question Number 72392 Answers: 0 Comments: 1
Question Number 72391 Answers: 0 Comments: 1
Question Number 72362 Answers: 1 Comments: 0
Question Number 72462 Answers: 0 Comments: 2
Question Number 72346 Answers: 0 Comments: 1

Question Number 72344 Answers: 0 Comments: 3
$${prove}\:{that}\:\:{e}^{{lnx}} \:=\:{x} \\ $$$${or}\:\:{a}^{{log}_{{a}} {x}} \:=\:{x} \\ $$
Question Number 72343 Answers: 0 Comments: 3
Question Number 72339 Answers: 0 Comments: 1
Question Number 72337 Answers: 1 Comments: 1
Question Number 72336 Answers: 0 Comments: 0
Question Number 72332 Answers: 1 Comments: 0
Question Number 72316 Answers: 0 Comments: 6
Question Number 72359 Answers: 1 Comments: 2

Question Number 72296 Answers: 1 Comments: 4
Pg 1404 Pg 1405 Pg 1406 Pg 1407 Pg 1408 Pg 1409 Pg 1410 Pg 1411 Pg 1412 Pg 1413
