
AllQuestion and Answers: Page 1408
Question Number 72563 Answers: 1 Comments: 1
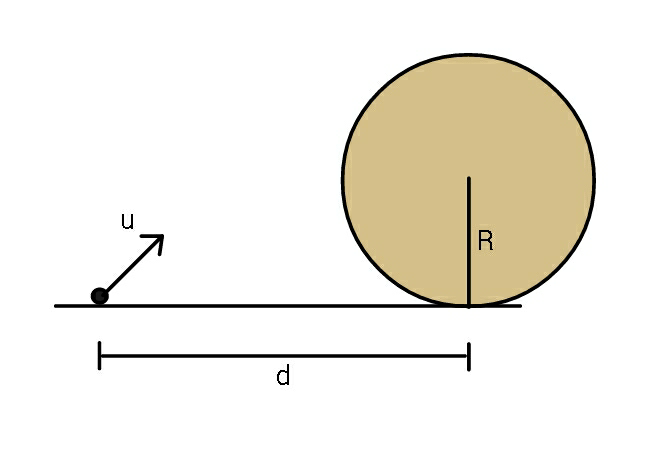
Question Number 72560 Answers: 0 Comments: 5

Question Number 72526 Answers: 2 Comments: 1
Question Number 72519 Answers: 1 Comments: 1
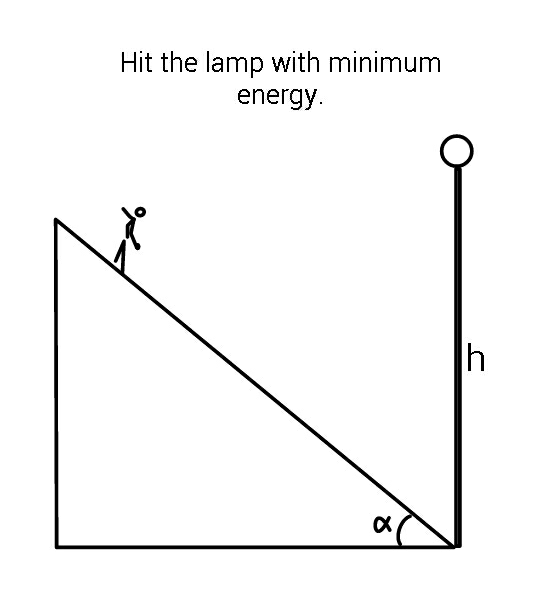
Question Number 72507 Answers: 0 Comments: 0
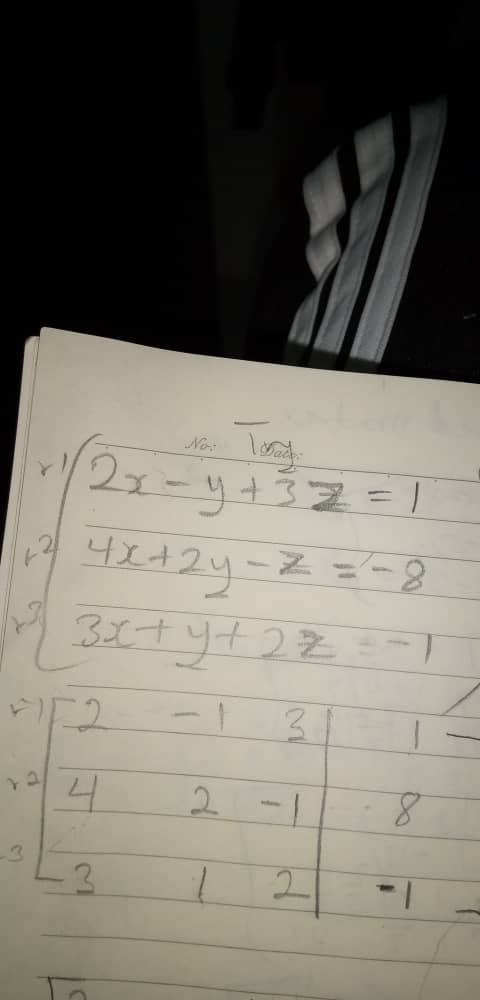
Question Number 72499 Answers: 3 Comments: 0
Question Number 72498 Answers: 1 Comments: 0
Question Number 72497 Answers: 3 Comments: 0
Question Number 72496 Answers: 2 Comments: 0
Question Number 72495 Answers: 0 Comments: 3
Question Number 72494 Answers: 1 Comments: 1
Question Number 72492 Answers: 3 Comments: 1
Question Number 72488 Answers: 2 Comments: 0
Question Number 72483 Answers: 2 Comments: 0
Question Number 72479 Answers: 0 Comments: 1
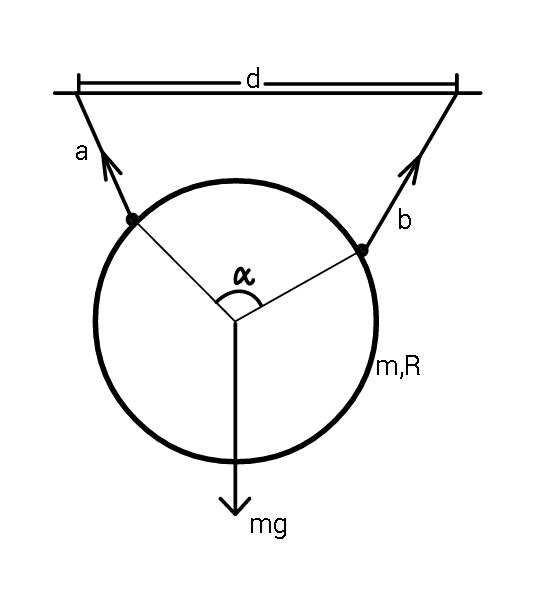
Question Number 72466 Answers: 1 Comments: 2
Question Number 72458 Answers: 0 Comments: 0

Question Number 72453 Answers: 0 Comments: 0

Question Number 72447 Answers: 1 Comments: 0
Question Number 72434 Answers: 1 Comments: 0

Question Number 72435 Answers: 0 Comments: 1
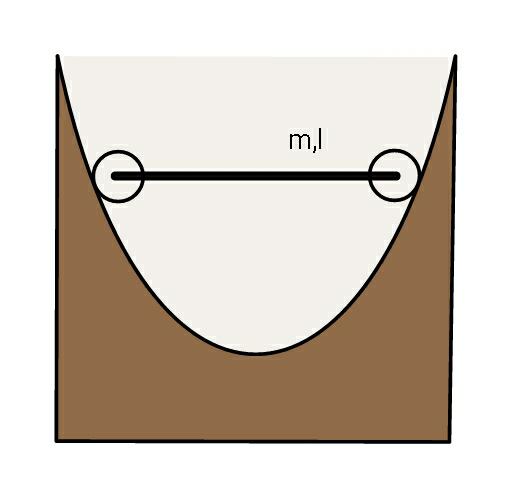
Question Number 72430 Answers: 0 Comments: 0
Question Number 72445 Answers: 0 Comments: 0
$$\int\frac{{x}\:{cos}\left({ax}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx} \\ $$
Question Number 72443 Answers: 1 Comments: 0
Question Number 72441 Answers: 2 Comments: 1
$$\mathrm{If}\:^{{n}} {C}_{\mathrm{12}} =\:^{{n}} {C}_{\mathrm{8}} \:,\:\mathrm{then}\:{n}= \\ $$
Question Number 72439 Answers: 0 Comments: 1

Pg 1403 Pg 1404 Pg 1405 Pg 1406 Pg 1407 Pg 1408 Pg 1409 Pg 1410 Pg 1411 Pg 1412
