
AllQuestion and Answers: Page 1407
Question Number 72721 Answers: 1 Comments: 12

Question Number 72718 Answers: 0 Comments: 3
Question Number 72689 Answers: 1 Comments: 0
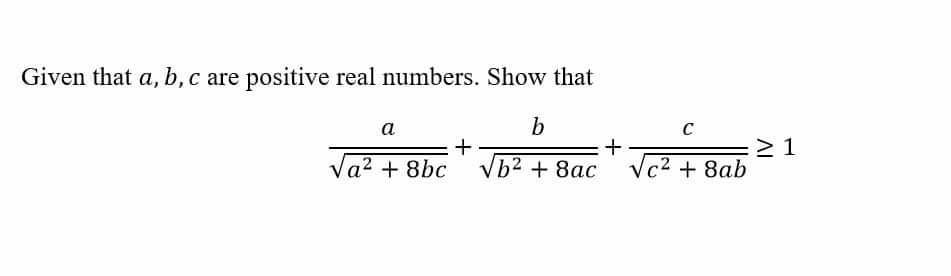
Question Number 72688 Answers: 3 Comments: 0
Question Number 72672 Answers: 2 Comments: 2

Question Number 72671 Answers: 0 Comments: 1

Question Number 72694 Answers: 0 Comments: 3
Question Number 72693 Answers: 1 Comments: 0
Question Number 72668 Answers: 1 Comments: 0

Question Number 72665 Answers: 1 Comments: 5
Question Number 72641 Answers: 0 Comments: 2

Question Number 72640 Answers: 3 Comments: 0

Question Number 72639 Answers: 1 Comments: 0
Question Number 72634 Answers: 1 Comments: 4
Question Number 72633 Answers: 0 Comments: 0
Question Number 72666 Answers: 1 Comments: 0
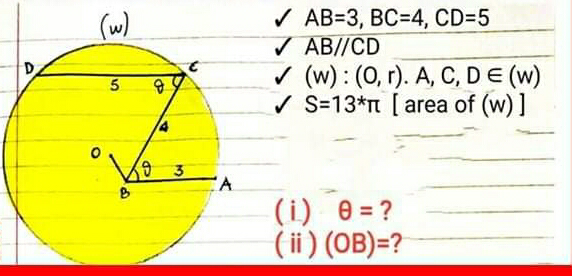
Question Number 72628 Answers: 0 Comments: 2
Question Number 72608 Answers: 1 Comments: 0

Question Number 72606 Answers: 2 Comments: 0
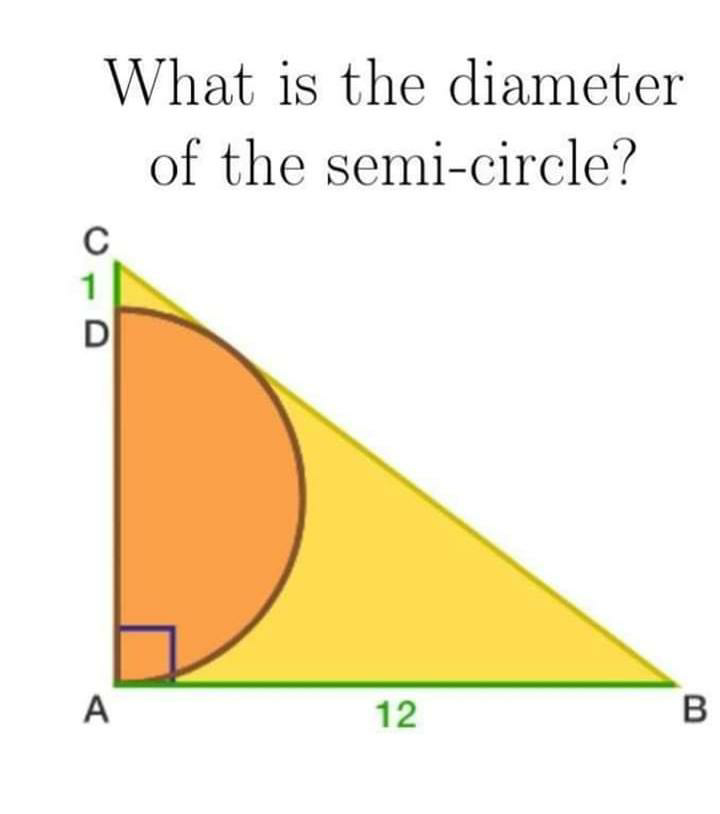
Question Number 72603 Answers: 1 Comments: 0

Question Number 72595 Answers: 1 Comments: 3
Question Number 72593 Answers: 2 Comments: 0
Question Number 72589 Answers: 0 Comments: 2
Question Number 72577 Answers: 0 Comments: 3
Question Number 72579 Answers: 1 Comments: 0

Question Number 72569 Answers: 3 Comments: 0
Pg 1402 Pg 1403 Pg 1404 Pg 1405 Pg 1406 Pg 1407 Pg 1408 Pg 1409 Pg 1410 Pg 1411
