
AllQuestion and Answers: Page 1405
Question Number 72990 Answers: 1 Comments: 1
Question Number 72988 Answers: 1 Comments: 1
Question Number 72986 Answers: 0 Comments: 0
Question Number 72965 Answers: 1 Comments: 1
Question Number 72952 Answers: 2 Comments: 4

Question Number 72931 Answers: 2 Comments: 0
Question Number 72930 Answers: 1 Comments: 0
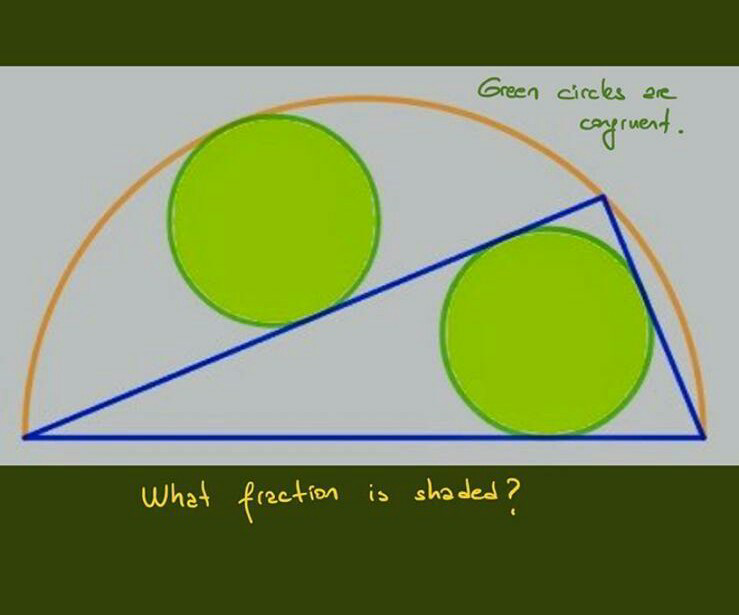
Question Number 73012 Answers: 4 Comments: 0
Question Number 72912 Answers: 1 Comments: 0
Question Number 72908 Answers: 2 Comments: 15
Question Number 72900 Answers: 1 Comments: 0
Question Number 72888 Answers: 1 Comments: 5
Question Number 72886 Answers: 1 Comments: 0
Question Number 72884 Answers: 0 Comments: 1
Question Number 72883 Answers: 1 Comments: 0
Question Number 72889 Answers: 1 Comments: 1
Question Number 72880 Answers: 0 Comments: 0

Question Number 72877 Answers: 0 Comments: 1
Question Number 72871 Answers: 1 Comments: 0

Question Number 72863 Answers: 0 Comments: 1

Question Number 72905 Answers: 2 Comments: 3
Question Number 72894 Answers: 1 Comments: 0

Question Number 72841 Answers: 1 Comments: 3
Question Number 72838 Answers: 0 Comments: 1
Question Number 72837 Answers: 0 Comments: 1
Question Number 72836 Answers: 1 Comments: 1

Pg 1400 Pg 1401 Pg 1402 Pg 1403 Pg 1404 Pg 1405 Pg 1406 Pg 1407 Pg 1408 Pg 1409
