
AllQuestion and Answers: Page 1404
Question Number 73059 Answers: 1 Comments: 3
Question Number 73057 Answers: 1 Comments: 0
Question Number 73056 Answers: 0 Comments: 1
Question Number 73055 Answers: 0 Comments: 0
Question Number 73052 Answers: 1 Comments: 0
Question Number 73051 Answers: 0 Comments: 1
Question Number 73049 Answers: 0 Comments: 0
Question Number 73048 Answers: 0 Comments: 0
Question Number 73047 Answers: 1 Comments: 0
Question Number 73046 Answers: 1 Comments: 0
Question Number 73045 Answers: 0 Comments: 0
Question Number 73044 Answers: 0 Comments: 0
Question Number 73043 Answers: 1 Comments: 2
Question Number 73042 Answers: 1 Comments: 0
Question Number 73041 Answers: 1 Comments: 1
Question Number 73040 Answers: 1 Comments: 0
Question Number 73039 Answers: 1 Comments: 0
Question Number 73037 Answers: 1 Comments: 1
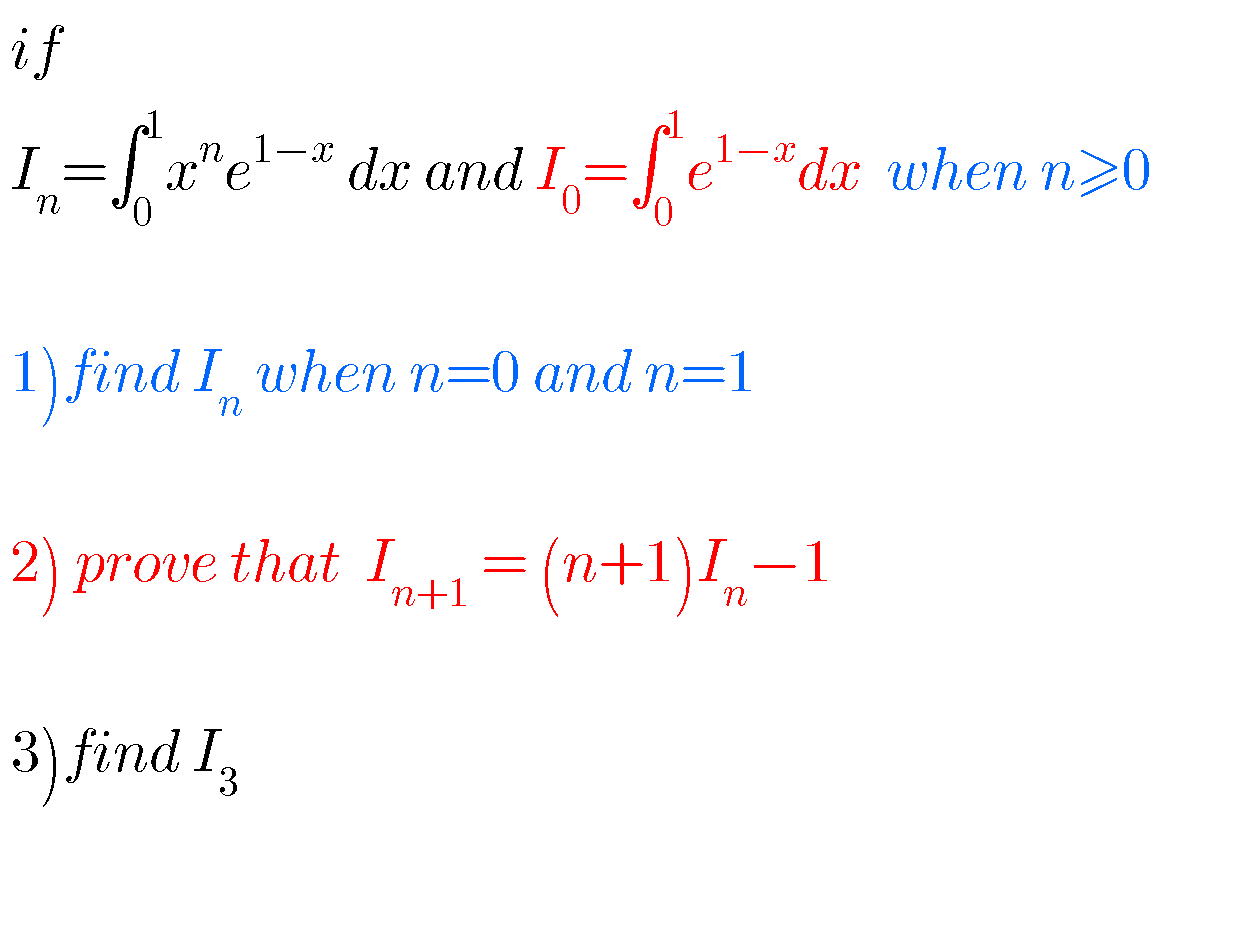
Question Number 73036 Answers: 1 Comments: 3
Question Number 73035 Answers: 0 Comments: 0
Question Number 73034 Answers: 1 Comments: 1
Question Number 73033 Answers: 1 Comments: 0
Question Number 73032 Answers: 1 Comments: 0
Question Number 73031 Answers: 0 Comments: 0
Question Number 73030 Answers: 2 Comments: 0

Question Number 73029 Answers: 1 Comments: 0
Pg 1399 Pg 1400 Pg 1401 Pg 1402 Pg 1403 Pg 1404 Pg 1405 Pg 1406 Pg 1407 Pg 1408
