
AllQuestion and Answers: Page 1403
Question Number 73221 Answers: 1 Comments: 0

Question Number 73210 Answers: 1 Comments: 2

Question Number 73203 Answers: 0 Comments: 1

Question Number 73202 Answers: 2 Comments: 3
Question Number 73200 Answers: 0 Comments: 4
Question Number 73258 Answers: 1 Comments: 0

Question Number 73191 Answers: 1 Comments: 0
Question Number 73251 Answers: 1 Comments: 0
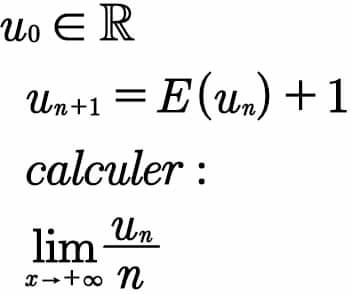
Question Number 73188 Answers: 0 Comments: 0

Question Number 73182 Answers: 0 Comments: 3
Question Number 73181 Answers: 1 Comments: 1
Question Number 73180 Answers: 0 Comments: 0
Question Number 73179 Answers: 1 Comments: 1
Question Number 73178 Answers: 1 Comments: 0
Question Number 73160 Answers: 1 Comments: 0
$$\mathrm{1}+{tanAtan}\frac{{A}}{\mathrm{2}}={tanAcot}\frac{{A}}{\mathrm{2}}−\mathrm{1}={secA} \\ $$
Question Number 73155 Answers: 0 Comments: 0
Question Number 73147 Answers: 1 Comments: 1
$$\int\frac{{x}−\mathrm{6}}{{x}^{\mathrm{3}} +\mathrm{1}}{dx} \\ $$$$ \\ $$
Question Number 73144 Answers: 1 Comments: 1
Question Number 73137 Answers: 0 Comments: 8

Question Number 73131 Answers: 0 Comments: 2
Question Number 73117 Answers: 2 Comments: 1
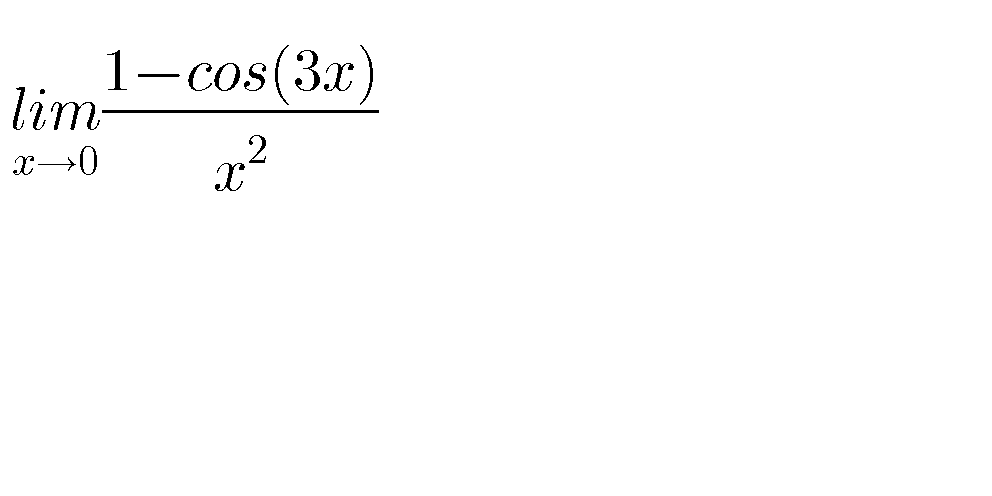
Question Number 73111 Answers: 1 Comments: 0

Question Number 73113 Answers: 1 Comments: 3
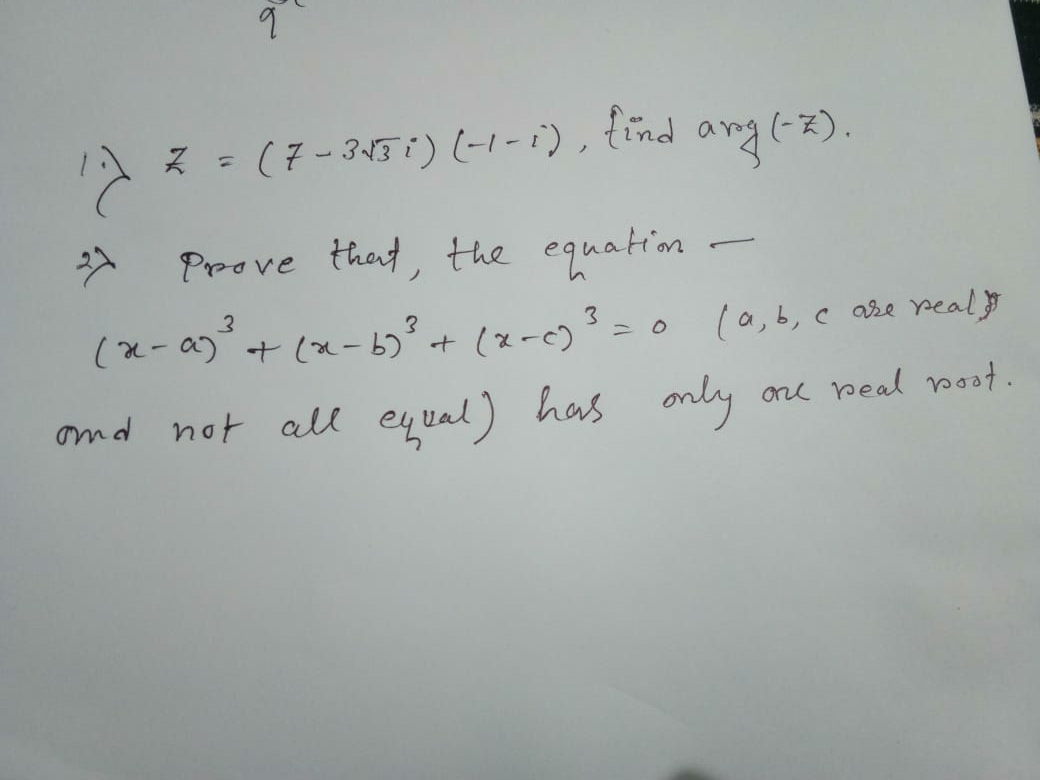
Question Number 73090 Answers: 2 Comments: 1

Question Number 73211 Answers: 0 Comments: 0
Question Number 73080 Answers: 1 Comments: 0
$$\mathrm{y}''=\mathrm{e}^{\mathrm{y}} \\ $$$$\mathrm{pls}\:\mathrm{solve} \\ $$
Pg 1398 Pg 1399 Pg 1400 Pg 1401 Pg 1402 Pg 1403 Pg 1404 Pg 1405 Pg 1406 Pg 1407
