
AllQuestion and Answers: Page 1401
Question Number 73411 Answers: 2 Comments: 2
Question Number 73406 Answers: 0 Comments: 0
Question Number 73405 Answers: 0 Comments: 0
Question Number 73399 Answers: 3 Comments: 1
Question Number 73397 Answers: 1 Comments: 1
Question Number 73396 Answers: 1 Comments: 1
Question Number 73378 Answers: 0 Comments: 3
Question Number 73358 Answers: 0 Comments: 1
$$\mathrm{1}/\mathrm{4}{x}\mathrm{2}−\mathrm{1}/\mathrm{2}{x}−\mathrm{13}=\mathrm{0} \\ $$
Question Number 73356 Answers: 0 Comments: 2
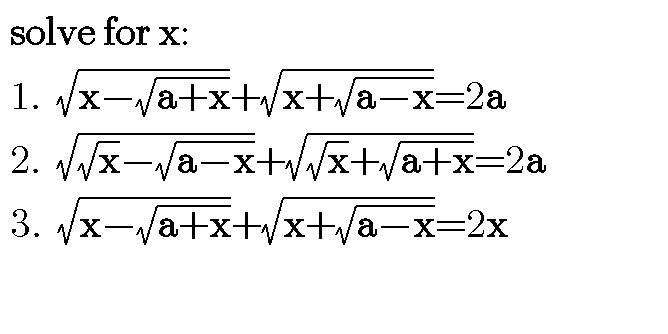
Question Number 73347 Answers: 0 Comments: 0

Question Number 73346 Answers: 3 Comments: 5

Question Number 73340 Answers: 0 Comments: 2
Question Number 73338 Answers: 0 Comments: 1
Question Number 73337 Answers: 0 Comments: 3
Question Number 73336 Answers: 1 Comments: 1
$${find}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} {ln}\left(\mathrm{1}+{e}^{{t}} \right){dt} \\ $$
Question Number 73335 Answers: 1 Comments: 2
Question Number 73334 Answers: 1 Comments: 0
Question Number 73333 Answers: 0 Comments: 1
Question Number 73332 Answers: 0 Comments: 0
Question Number 73331 Answers: 0 Comments: 1
Question Number 73330 Answers: 1 Comments: 1
Question Number 73327 Answers: 0 Comments: 1
Question Number 73308 Answers: 0 Comments: 6
Question Number 73297 Answers: 2 Comments: 1

Question Number 73295 Answers: 1 Comments: 0
Question Number 73293 Answers: 2 Comments: 2
Pg 1396 Pg 1397 Pg 1398 Pg 1399 Pg 1400 Pg 1401 Pg 1402 Pg 1403 Pg 1404 Pg 1405
