
AllQuestion and Answers: Page 1398
Question Number 73745 Answers: 0 Comments: 0
Question Number 73744 Answers: 0 Comments: 0
Question Number 73737 Answers: 2 Comments: 1

Question Number 73736 Answers: 1 Comments: 0
Question Number 73730 Answers: 2 Comments: 0
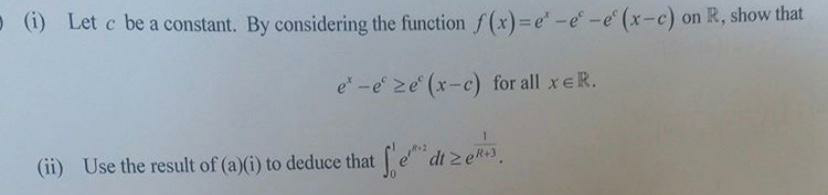
Question Number 73725 Answers: 0 Comments: 0

Question Number 73724 Answers: 0 Comments: 0
$${find}\:{all}\:{simple}\:{graphical}\:{sequence}\:{for}\:{n}=\mathrm{4} \\ $$
Question Number 73723 Answers: 0 Comments: 0
Question Number 73722 Answers: 0 Comments: 2

Question Number 73721 Answers: 0 Comments: 0

Question Number 73715 Answers: 1 Comments: 2
Question Number 73710 Answers: 0 Comments: 0

Question Number 73709 Answers: 0 Comments: 0

Question Number 73708 Answers: 0 Comments: 0

Question Number 73707 Answers: 0 Comments: 1

Question Number 73706 Answers: 1 Comments: 0
Question Number 73712 Answers: 1 Comments: 0

Question Number 73697 Answers: 1 Comments: 1
$${find}\:{a}\:{formulae}\:{for}\:{calculus}\:{of}\:{arctan}\left({x}+{iy}\right) \\ $$
Question Number 73689 Answers: 2 Comments: 0
Question Number 73679 Answers: 0 Comments: 1
Question Number 73673 Answers: 2 Comments: 3

Question Number 73671 Answers: 0 Comments: 0

Question Number 73668 Answers: 1 Comments: 0
Question Number 73665 Answers: 1 Comments: 0
Question Number 73663 Answers: 1 Comments: 0

Question Number 73649 Answers: 1 Comments: 2
Pg 1393 Pg 1394 Pg 1395 Pg 1396 Pg 1397 Pg 1398 Pg 1399 Pg 1400 Pg 1401 Pg 1402
